Как заработать в Binomo
Binomo относится к очень популярной среди трейдеров категории брокеров бинарных опционов, предлагающих начать торговлю с относительно небольшой суммы денег. Одной из важных особенностей компании является наличие российской лицензии (ЦРОФР), обеспечивающей клиентам организации спокойствие на бинарном рынке.
Минимальный счет у Binomo всего $10, а стоимость бинарных опционов начинается от $1. Можно открывать депозит еще в евро или даже российских рублях, кому как удобнее. Обзор брокерской компании с отзывами трейдеров Вы найдете вот здесь. На этот раз я расскажу об эффективном способе заработка в Binomo, которым сложно воспользоваться у большинства других брокеров на бинарном рынке.
В чем же такая особенность брокера Биномо? Она заключается в возможности приобретать бинарные опционы стоимостью от $1, что очень пригодится в том методе заработка, о котором буду рассказывать в этом обзоре.
https://binomo.com/ru — официальный сайт брокера Binomo.
Как зарабатывают у брокера Binomo
Вы обращали внимание, что цена на рынке все время колеблется? Она может «топтаться» практически на месте продолжительное время, или же начать быстро расти, а потом оперативно развернуться в обратную сторону. Редко, когда бывает, что бы рынок постоянно падал, не корректируясь вверх или наоборот, постоянно рос, не откатывая вниз, хотя бы на недолгое время.
Такое наблюдение позволило спекулянтам воспользоваться системой мартингейл, разработанной более 100 лет назад, для торговли бинарными опционами. Об обстоятельствах появления мартингейл можно найти различные предположения, но одним из самых популярных является точка зрения, что данная система впервые была разработана для игры в рулетку.
Теперь переходим к сути способа заработка на бинарных опционах. Мы можем себе позволить заключить сделку по приобретению бинарного опциона, чуть ли не наугад, но для приличия возьмем за правило, что контракт приобретается против текущего тренда при первых признаках его разворота:
На иллюстрации выше видно, что на рынке наблюдался восходящий тренд, после чего цена стала колебаться в диапазоне и «крениться» вниз. В этот момент мы можем приобретать бинарный опцион «ниже», соответствующий следующим требованиям:
В этот момент мы можем приобретать бинарный опцион «ниже», соответствующий следующим требованиям:
- актив должен быть высокодоходным, например, EURUSD;
- время исполнения выбрать (обдумать) заранее, но рекомендую для начала, что бы не торопиться и не запутаться в действиях, остановиться на варианте 3 минуты;
- для заработка в Binomo следует для начала выбирать минимальную стоимость опциона ($1).
Сделка либо принесет нам деньги, либо окажется убыточной, тогда мы потеряем средства, затраченные на покупку бинарного опциона ($1). В первом случае все понятно, если контракт принес прибыль, мы просто будем ждать следующего момента с трендом и началом коррекции. С другой стороны, как быть, если наша операция завершилась неудачей, забыть о ней и дожидаться нового сигнала?
Эффективная торговля в Binomo
Просто так забывать про убытки мы не станем, а начнем использовать в своих интересах даже, на первый взгляд, неудачные ситуации. Как только бинарный опцион исполнится через 3 минуты после покупки, унеся с собой наш $1, мы тут же приобретем новый контракт, направленный вниз («ниже»), со временем до экспирации 3 минуты, но уже за $2.
Обратите внимание, что второй бинарный опцион приобретается сразу, как только закрылась с потерями предыдущая сделка. Нам уже не нужно даже смотреть на рынок, ведь направление контракта определено, оно должно совпадать с направлением закрытого опциона (в данном примере «ниже»). Время исполнения так же желательно выбрать прежнее (3 минуты) или близкое по величине.
| Чтобы заработать у Binomo по данной стратегии, нам достаточно дождаться даже хотя бы непродолжительного разворота цены. Бывает, что приходится заключить несколько сделок подряд, прежде чем рынок войдет в коррекцию и наша сделка | закроется с прибылью. В этом случае каждый последующий бинарный опцион выбирается дороже предыдущего, ведь прибыли по удачно закрытой сделке должно хватать на покрытие потерь, образованных неудачными операциями. |
Например, купили опцион за $1, потом за $2, затем за $5, который, в отличие от предыдущих, закрылся с профитом. Пусть доходность была 80%, а значит, наша прибыль со сделки $4 (из них $3 нужны для того, что бы перекрыть потери = $1+$2).
Не забудьте заранее рассчитать, какой стоимости должен быть каждый последующий опцион, чтобы прибыли с него хватило на покрытие потерь и обеспечение профита. Чтобы произвести такие расчеты, Вам нужно будет знать, какова доходность по активу, который решите использовать в работе (рекомендую EURUSD, ведь у него самые высокие проценты вознаграждения).
В некоторых рыночных ситуациях тремя сделками не отделаться, так что будьте готовы, что иногда может понадобиться приобрести 5-6 бинарных опционов подряд для успешного закрытия серии. Еще хотел бы предупредить о двух распространенных ошибках среди трейдеров, зарабатывающих у брокера Binomo данным способом:
- не жадничайте, не завышайте стоимость первой сделки, ведь именно от нее будет зависеть цена каждого последующего опциона в серии;
- перед началом торговли обязательно просмотрите календарь экономических событий на предмет важных новостей в ближайшее время.
Дело в том, что новость может оказаться причиной возникновения сильного тренда, против которого становиться на рынке крайне нежелательно. Так что, убедитесь в отсутствии новостей, а только потом приступайте к работе. Эти правила (про жадность и новости) помогут Вам торговать более стабильно и избегать неприятных серий сделок.
https://binomo.com/ru — официальный сайт брокера Binomo.
Теперь Вы знаете, как можно эффективно торговать в Binomo и зарабатывать на этом вполне приличные деньги. Способ уже довольно старый и проверенный, так что на него можно полагаться в своей торговле. Рекомендую начинать именно с пары EURUSD, сделок по $1 и с экспирации в 3-5 минут на контракт.
Как заработать на бинарных опционах для начинающих
Как заработать на бинарных опционах или бинарные опционы для начинающих
Рынок бинарных опционов – один из самых прогрессивных финансовых рынков мира. Да, мы это слышали! Но что нам дают брокерские компании бинарных опционов, для того, чтобы мы зарабатывали на этом рынке? Примитивную платформу с маленьким окошком котировок, как смотровое окошко в танке, котировки, взятые невесть откуда, отсутствие индикаторов для торговли и проскальзывание в несколько пунктов на каждой сделке. Получается, что рынок есть, а зарабатывать на нем ох как сложно. Именно поэтому шаги, сделанные компанией Binomo можно назвать революционными!
В этом разделе Вы узнаете как заработать на бинарных опционах. Также на этой странице мы хотим по порядку рассмотреть организационные вопросы, связанные с регистрацией торгового счета, верификацией Вашего аккаунта и выводом прибыли на различные платежные средства.
Стоит отметить, что в первую очередь, наши инструкции по бинарным опционам для начинающих трейдеров. В рамках инструкций для новичков здесь будут разобраны действительно важные аспекты трейдинга на бинарных опционах и в доступной форме представлены Вам.
Почему Binomo – это революция
Первое, почему брокер Binomo выделяется из толпы брокерских компаний, работающих в Рунете – это его торговая платформа. На фоне того, как большинство других брокеров предлагают нам заключать сделки бинарными опционами с помощью однообразных торговых платформ, в которых:
- Маленькое окно терминала не позволяющее увидеть полную картину рынка – то есть, проанализировать динамику движения цены.
- Отсутствие технических индикаторов, которые повышают возможность получить точный сигнал на открытие сделок.
- Сделки открываются с запаздыванием и проскальзыванием, а трейдеры теряют драгоценные пункты, которых, как обычно, не хватает для получения прибыли по сделке.

- Между опционами присутствуют «мертвые» зоны, которые не дают возможность заключить сделку по нужной цене.
Этот перечень можно было бы продолжать и дальше, но и этого достаточно для того, чтобы ваша торговля была убыточной. Что предложил брокер Binomo? Новая платформа Binomo – это торжество на фоне остальных торговых терминалов брокеров бинарных опционов!
Новая платформа Binomo
Рассмотрим новую платформу Binomo более подробно. Торговый терминал разработан брокером самостоятельно с привлечением опытных специалистов извне. В результате многомесячной разработки на сайте брокера появилась платформа, в которой реализовано все то, чего так не хватает остальным торговым терминалам рынка, а именно:
- Скорость заключения сделок поставлена на новый уровень и теперь составляет 5 миллисекунд, то есть – моментально. А значит, на новой платформе Binomo сделки не проскальзывают, а трейдер заключает торговые позиции именно в том месте, в котором планировал.
- В новую платформу Binomo включены технические индикаторы, то есть, трейдеры получили возможность создавать торговые системы, не выходя из платформы и не пользуясь иными сервисами.
- Технология трейдинга построена на принципе Non-stop. «Мертвые» зоны исключены со сроков заключения сделок. Иными словами, на новой платформе Binomo сделки можно заключать в любой момент времени.
- Котировки поставляются от агентства с мировым именем – Thomson Reuters.
- Окно торговой платформы теперь занимает весь экран монитора трейдера и позволяет запросто сделать анализ динамики движения актива. А значит – заключить сделку в нужную сторону.
- Котировки представлены в виде японских свечей и позволяют в торговле использовать системы торговли по свечным паттернам.
- Прибыльность опционов Binomo составляет до 87%.
- Торговать можно сделками размером от $1, а торговый счет пополнить на сумму от $10 (есть и рублевые счета).
- И самое главное новая платформа Binomo содержит бездепозитные бинарные опционы, но об этом чуть ниже отдельно.

Регистрация торгового счета у брокера
Самое время поговорить и увидеть поближе над чем так долго трудились основатели компании. Начнем с регистрации Вашего торгового счета. Для открытия счета у брокера Вам понадобится только заполнить необходимые поля формы регистрации на сайте. Для этого перейдите на главную страницу сайта брокера Binomo, где в правом углу экрана найдите шаблон для регистрации:
или воспользуйтесь формой ниже в этой статьи.
Важно, чтобы Вы указали действующий почтовый адрес, т.к. именно на него Вы будете получать важную информацию от брокера, текущие предложения и, что важно, при выводе прибыли на почтовый адрес, будет высылаться актуальная информация о текущем состоянии Вашего запроса на вывод прибыли.
Впишите свои личные данные для создания лицевого счета:
Очень большим плюсом данной компании является отсутствие звонящих менеджеров в отличии от других компаний. Вы сможете получать поддержку тогда, когда это удобно вам и никто не будет докучать с просьбами вложить деньги, чтобы получить какие либо привилегии от брокера. Все привилегии у брокера вы получите абсолютно БЕСПЛАТНО!
Далее выбираем валюту депозита, которой желаете торговать на новой платформе Binomo:
Почему брокер Binomo?
Возможно для кого то перечисленных удобств будет мало и возможность торговать без пополнения для кого то всего лишь хорошая возможность изучить платформу. Но позвольте объяснить почему мы решили взять платформу Binomo в качестве примера по открытию счета для начинающих. Ниже мы перечислили ряд причин почему, мы считаем эту платформу лучшей для торговли в 2016 году:
Платформа регулируется ЦРОФР
Минимальная сделка всего 1$
Высокий процент выплат: до 100%
Наличие большого количества БЕСПЛАТНЫХ обучающих материалов
Ежедневные обзоры рынка, доступные всем активным трейдерам
Возможность получить 20 бесплатных сделок без пополнения
Возврат потерь до 30%
В форме ниже вы сможете пройти быструю регистрацию и получить первые
20 сделок бесплатно.
Итак, на новой платформе Binomo вы найдете не только бинарные опционы от $1, которые позволяют торговать с минимальными рисками, но и бездепозитные бинарные опционы, с которыми можно начать торговать с нуля. Пусть это звучит невероятно, но это действительно так!
После регистрации на сайте этой компании вам автоматически зачисляется на торговый счет 20 сделок, которые вы можете заключить за счет Binomo и самое главное, внимание – еще до момента пополнения торгового счета!
Эта акция является бессрочной и не является бонусом. Вы торгуете без капиталовложений за счет брокера, а всю полученную прибыль имеете право вывести себе. Либо потом вложить в заключение будущих сделок. То есть, не имея цента за душой можно прийти к Биномо и, воспользовавшись бездепозитными бинарными опционами, заработать на заключение будущих сделок!
Как пополнить торговый счет у Биномо?
Если вы уже использовали свою возможность торговать без пополнения и готовы к серьезной торговли этот раздел инструкций для Вас. После прохождения регистрации, для начала торговли нам нужен положительный баланс, и мы переходом к разделу «Касса». Перед нами открывается масса возможностей для пополнения депозита.
После выбора удобного для вас способа пополнения Вам необходимо указать сумму, на которую Вы пополните счет, или выбираете ниже предлогаемые суммы для внесения депозита.
Способ №1: Кредитная карта. поменять
Этот вариант работает как стандартный электронный платеж. Вы указываете 16-ти значный номер, который указан на лицевой стороне карты, и ее срок действия, затем Вы вписываете в соответствующие поля имя и фамилию держателя карты. После чего Вам нужно указать трехзначный CVV код безопасности с обратной стороны карты, и можно пополнять баланс!
Способ №2: Электронные платежные системы
Брокер предоставляет возможным пополнение через кошелек Qiwi. Следующими в списке находяться Яндекс деньги, wenmoney и Neteller. Также брокер Биномо предоставляет возможность пополнить торговый счет с помощью баланса мобильного телефона. На этой странице выбрав удобный способ Вам необходимо указать нужную сумму и выбрать способ оплаты, после этого из кассы Вы автоматически попадете на страницу Вашего электронного кошелька, где после ввода своих идентификационных данных Вы сможете пополнить свой счет.
Также брокер Биномо предоставляет возможность пополнить торговый счет с помощью баланса мобильного телефона. На этой странице выбрав удобный способ Вам необходимо указать нужную сумму и выбрать способ оплаты, после этого из кассы Вы автоматически попадете на страницу Вашего электронного кошелька, где после ввода своих идентификационных данных Вы сможете пополнить свой счет.
После входа в кабинет Вы получаете доступ к торговой платформе. Здесь Вы можете торговать такими видами опционов, как «выше-ниже», «одно касание», «диапазон». Основным видом опциона является опцион «выше-ниже», а остальные – как производные от него. В терминале Вы найдете график движения цены и список активов, которые доступны для торговли.
Как получить прибыль на бинарных опционах
Заработать на бинарных опционах Вы можете, заранее определив направление цены актива. А для того, чтобы знать как торговать бинарными опционами прибыльно, нужно исходить из условий трейдинга. Различают исполнившийся опцион, с заранее определенной прибылью, и неисполнившийся с нулевым результатом.
Ну и вопрос, который интересует тех, кто первый раз столкнулся с бинарными опционами — как зарабатывать на опционном рынке? Как определить в какую сторону будут двигаться котировки актива – ВВЕРХ или ВНИЗ? С новой платформой Binomo этот процесс стал намного проще!
Для определения направления воспользуйтесь техническим анализом и инвестиционными идеями от профессионалов опционного рынка:
Задачей трейдера является определение направления движения цены любыми доступными ему способами (совокупность методов и стратегий анализа называют торговой системой). Покупая опцион в выбранном направлении, по истечению опциона Вы получаете результат в виде исполнившегося или неисполнившегося опциона, или простыми словами, Вы получаете прибыль или теряете сумму ставки.
В случае правильного прогноза вы получаете на торговый счет до 87% от суммы инвестиций. То есть, вложили в заключение сделки $100 и получили «выхлоп» $187. Как торговать бинарными опционами узнайте в разделе обучения сайта Binomo, где в бесплатном доступе содержится масса уникальной обучающей информации:
Как торговать бинарными опционами узнайте в разделе обучения сайта Binomo, где в бесплатном доступе содержится масса уникальной обучающей информации:
После того, как по результатам торгов Вы заработали прибыль и хотите вывести заработанные деньги, Вы можете сделать это в разделе «Банкинг» > «Вывод средств». Страница вывода средств выглядит следующим образом:
Заходим на страницу вывода средств и в поле сумма выплаты вносим сумму, которую хотим вывести. Вывод деньги обычно производится на то же средство с которого был произведен депозит. Это делается во избежание потери денег или несанкционированного вывода в случае подбора пароля или взлома вашей почты и проникновению посторонних лиц на ваш торговый счет. После выбора способа, мы оставляем один из комментариев для брокера, указывая причину вывода, так как данный брокер не занимается об звоном трейдеров. Выбираем один из вариантов: фиксирую прибыль, проверяю как работает вывод средств, не получается торговать, не устраивает компания или платформа. При выборе другое укажите причину, чтобы брокер смог вам подсказать как улучшить свои результаты.
После постановки средств на снятие, для завершения процесса регистрации и последующего вывода Ваших средств, Вы получаете на почту письмо-запрос на верификацию Вашего торгового аккаунта, в случае если вы не делали ее ранее. Произведите верификацию счета и подтвердите свою личность, после чего вывод средств будет производиться быстро и без лишних вопросов.
Теперь, когда Вы узнали, как заработать на бинарных опционах, самое время попробовать сделать это самостоятельно! Тем более, что всю необходимую информацию Вы можете найти на нашем ресурсе. А если что-то будет не понятно, Вы всегда можете связаться с нами через чат. Удачи!
Специальное предложение от компании PracticalBinary!!!
Страница не найдена | Practical Binary
Блог трейдера
На просторах интернета сегодня каждый может найти для себя любую сферу самореализации в финансовом
Блог трейдера
Бинарные опционы на сегодняшний день– это самый быстро развивающийся инструмент финансового рынка. Появление множества
Появление множества
Блог трейдера
Стремительно растущая популярность онлайн-трейдинга на рынке бинарных опционов стала причиной появления на бирже множества
Блог трейдера
Рынок Форекс продолжает развиваться, и теперь большая часть трейдеров отказывается от настольных терминалов в
Не так давно заявивший о себе брокер Daily-trades имеет большой потенциал, для того чтобы
Блог трейдера
Торговые сигналы форекс — это одна из видов услуг, которую могут предоставлять брокеры, трейдерские
Как зарабатывать в Биномо
Чарльз Доу сказал – «тренд – твой друг. Просто следуй за ним, и он приведет тебя куда нужно». Эта цитата стала основой торговли для многих трейдеров на рынке Форекс. Эффективность метода была многократно подтверждена успешными сделками с самыми разными активами и на различных площадках. По этому принципу были построены сотни стратегий, наполнение которых отличается техническими инструментами и мелкими нюансами, но суть всегда остается неизменной – торговля по тренду прибыльна!
По этому принципу были построены сотни стратегий, наполнение которых отличается техническими инструментами и мелкими нюансами, но суть всегда остается неизменной – торговля по тренду прибыльна!
Наиболее эффективен такой метод работы на бинарных опционах. Он позволяет правильно выверять время и количество сделок, увеличивая доход и минимизируя риски. Формирование тренда происходит под влиянием новостных и экономических факторов.
И если с первыми все ясно, так как выход важных для рынка новостей всегда запланирован, то в экономическом аспекте цена пребывает в состоянии контролируемого хаоса. Отслеживать самостоятельно экономические сигналы довольно сложно, особенно начинающему трейдеру, поэтому лучше использовать технические индикаторы. Удобнее всего это делать на платформе одного из крупнейших брокеров бинарных опционов – .
— получите дополнительные +25% к сумме пополнения счета!
Зарабатываем в Биномо, торгуя по тренду
Чтобы понять, как зарабатывать в Биномо торгую по тренду, нужно определиться с тем, какие они бывают. Есть два типа тенденций:
- Восходящая (бычья). Рынок движется вверх;
- Нисходящая (медвежья). Рынок опускается вниз.
Бычий тренд формируется под влиянием повышенного спроса на актив, что влечет его удорожание, тогда как медвежий – это результат обратной ситуации. Спрос превышает предложение, из-за чего цена актива падает. Стремление к балансу – это черта любой организованной системы, поэтому преобладание одного тренда рано или поздно прекращается, и начинается другой, либо тенденция отсутствует вовсе. Такое состояние рынка называется «флет», и это самое неблагоприятное время для торговли.
Для того чтобы правильно установить направление движения цены, используются таймфреймы Н12 и Н1. Первый нужен для выявления общей тенденции, а второй поможет определить момент входа в рынок. Чтобы зарабатывать в Биномо по данной стратегии, внизу экрана есть панель индикаторов.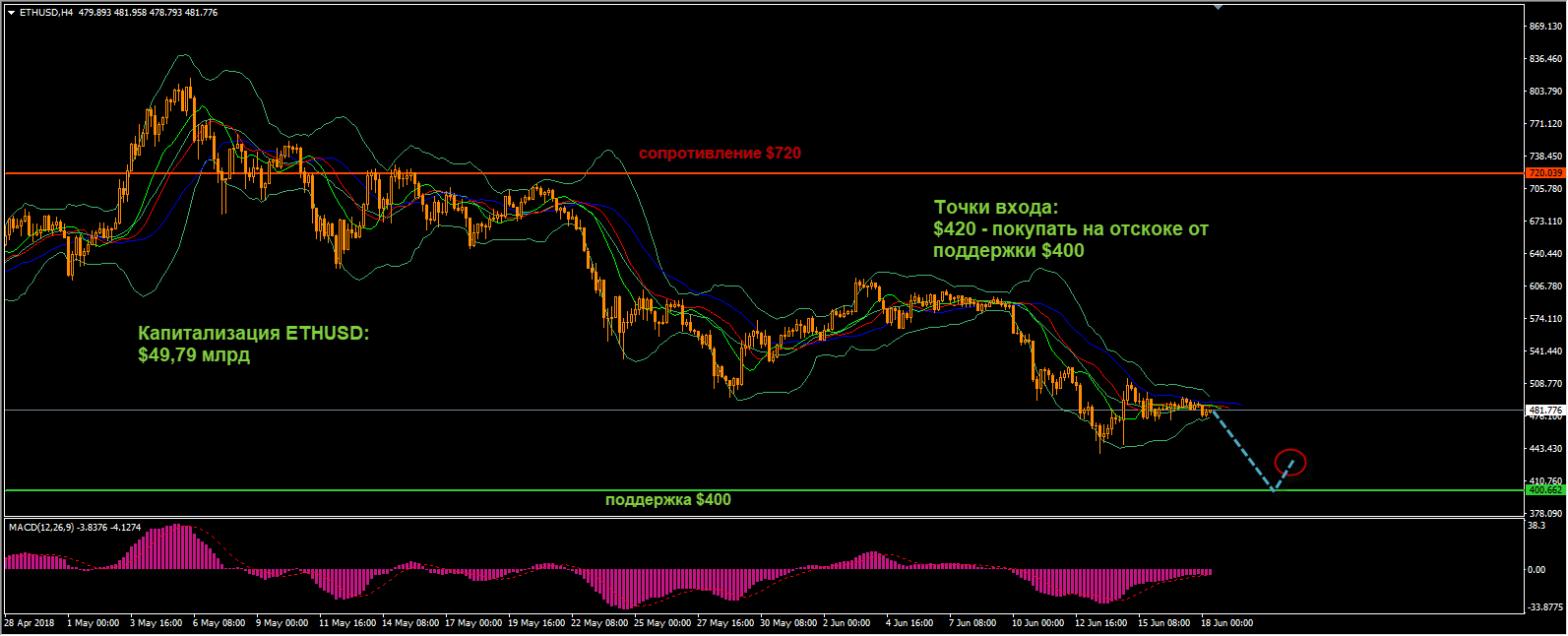
Определить направление тренда поможет МА(среднее скользящее). Он отображает усредненные показатели изменения цены и отсекает назойливый рыночный шум, а чтобы данные индикатора были более точными, лучше выбрать его экспоненциальное отображение относительно изменения цены. Подробнее с индикаторами в Биномо можно ознакомиться в отдельном разделе нашего сайта.
Правильно настроенный инструмент МА укажет на формирование тренда и его направление, позволив зарабатывать в Биномо.
Нюансы заработка в Биномо по тренду
Основным нюансом торговли бинарными опционами по тренду является необходимость расчета срока экспирации, или момента завершения действия контракта. Поэтому, прежде чем покупать опцион стоит обратить внимание на такие моменты, как:
- длительность тренда;
- наличие или отсутствие отката цены;
- расхождение графика с индикатором.
По первому пункту можно сказать, что тянущийся тренд, особенно на активах с высокой волатильностью, большая редкость. Чаще всего наблюдаются сменяющие друг друга микротренды, в которых тоже можно и нужно работать, но с осторожностью, и об этом говорит второй пункт.
Если график быстро растет или падает, и такое движение не сопровождается коррекцией, то вероятно произойдет скорый разворот тенденции. Не стоит покупать опцион в середине микротренда, так как срок экспирации контракта придется на изменение его направления и принесет убыток.
Чтобы разбираться, как зарабатывать в компании Биномо торгуя в микротрендах, нужно внимательно отслеживать движение средней скользящей МА. Экспоненциальный рост цены пропорционален ее значению, а значит, линия индикатора будет игнорировать кратковременные коррекции в период разворота или боковой тенденции. Выраженное устойчивое движение линии вверх или вниз, после коррекции или флета и будет сигналом для входа в рынок.
Подходящие активы
Для торговли по тренду лучше всего использовать классические бинарные опционы, доходность которых составляет минимум 80%.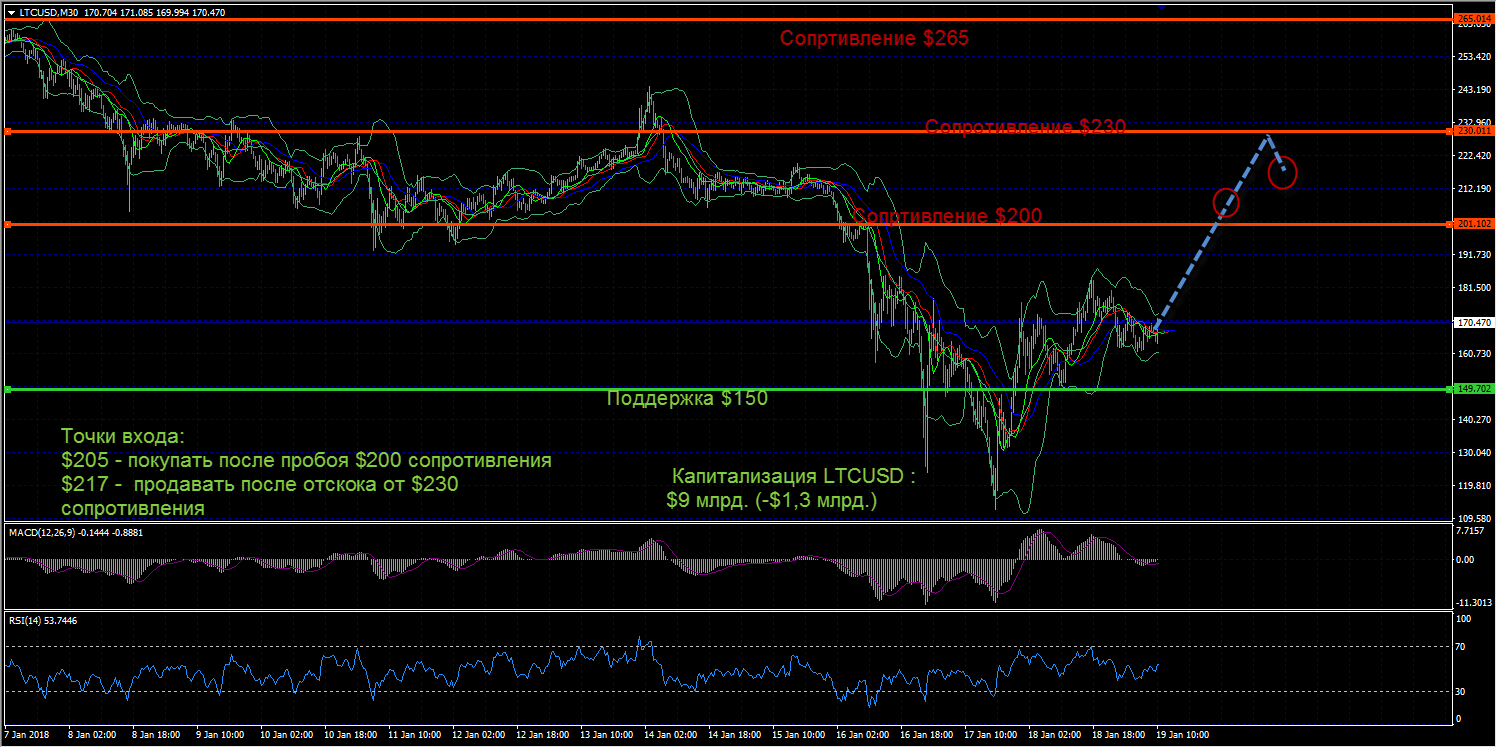 Из активов отлично подойдут валютные пары, как самый динамичный и востребованный инструмент торговли. Лучше всего использовать: EUR/USD, GBP/USD, USD/CHF, USD/JPY. Важно учитывать и время торговли, избегая периодов ценовой нестабильности активов, которые приходятся на моменты открытия и закрытия бирж.
Из активов отлично подойдут валютные пары, как самый динамичный и востребованный инструмент торговли. Лучше всего использовать: EUR/USD, GBP/USD, USD/CHF, USD/JPY. Важно учитывать и время торговли, избегая периодов ценовой нестабильности активов, которые приходятся на моменты открытия и закрытия бирж.
При покупке опционов на валютные пары, средний размер сделки не должен превышать 5% от депозита, иначе несколько неудачных операций подряд не позволят использовать метод Мартингейла. То есть, при минимальном депозите в 200$-250$, сумма бинарного контракта может составлять 10$-15$, но не больше.
— официальный сайт брокера Binomo.
Используем Мартингейл и тренд для заработка в Binomo
Открытие позиции по тренду считается самым безопасным способом зарабатывать в Биномо, но и здесь возможны неожиданности. Цена актива формируется под влиянием многих факторов, учесть их в полном объеме невозможно. Поэтому случается так, что вместо ожидаемого роста, рынок начинает падать, или наоборот.
В таком случае на помощь приходит метод Мартингейла, который позволяет компенсировать потери от неудачных сделок, путем последовательного увеличения ставки. Применять его нужно, только если соблюдены правила торговли по тренду, в противном случае, кратное увеличение ставки приведет к «сливу» депозита.
Увеличивать сумму контракта стоит при затянувшейся коррекции, которая возможна после быстрого развития тенденции. В таком случае метод Мартингейла не только компенсирует потери от неудачных сделок, но и оставит положительный баланс на депозите. Такой способ возмещения потерь можно использовать во время всего периода торгов. Важно лишь учитывать возможности депозита, сумма которого должна покрывать минимум 6 неудачных сделок.
Заключение
Открытие позиций по тренду – это универсальная рыночная стратегия, которая уже много лет демонстрирует свою эффективность и безопасность для депозита. Простые правила применения дополняются техническими индикаторами, что в совокупности дает возможность прогнозировать движение цены с высокой точностью, а метод Мартингейла позволяет избежать серьезных финансовых потерь.
Можно ли заработать на бинарных опционах
Сегодня в Интернете можно найти огромное количество вариантов дополнительного заработка, среди которых особо привлекательным выглядят бинарные опционы. Максимальная доходность до 90% и простой алгоритм применения сегодня делают данный инструмент не только очень популярным, а и очень скандальным, ведь именно с помощью бинарных опционов очень часто «разводят» аудиторию Рунета. Таким образом, невольно возникает вопрос — стоит ли торговать бинарными опционами, можно ли заработать на этом? И сегодня мы расскажем не только о том, почему бинарные опционы способны приносить реальную прибыль, а и продемонстрируем, как правильно использовать данный финансовый инструмент.
Фантастический доход за несколько минут
Среди известных биржевых инструментов, бинарные опционы являются наиболее простым. Основная задача трейдера – правильно спрогнозировать тенденцию колебаний стоимости актива в определенной временной перспективе. То есть, здесь не имеет значения количество преодоленных ценой пунктов, ведь даже один пункт в спрогнозированном направлении способен принести до 90% прибыли на одной сделке! Более того – получать прибыль можно ежеминутно, ведь устанавливать длительность сделки можно самостоятельно из диапазона 1 минута – 1 час.
Фактически, похвастаться такой простотой и прибыльностью не способен больше ни один биржевой продукт. Единственными вопросами теперь остаются подходящая торговая площадка и как разобраться в торговом процессе начинающему трейдеру.
Как выбрать брокерскую компанию
Сперва решим вопрос с брокерской компанией, а точнее – как не стать жертвой ее обмана. Поскольку финансовый рынок является средой обитания огромных денежных сумм, не удивляет, что здесь развелось очень много мошенников. Поэтому, при выборе торговой площадки необходимо тщательно анализировать предоставляемые брокером сервисы.
Мы провели сравнительный анализ торговых условий и сервисов многих брокерских компаний и среди них выбрали для тестирования реальной доходности бинарных опционов брокера Binomo.
Свой выбор мы сделали по ряду следующих причин:
- Компания позволяет начать торговлю с 10 USD на торговом счету, при этом сумма минимальной сделки составляет – 1 USD. То есть, даже если новичку сперва не получится торговать и попросту не понравятся бинарные опционы, такая сумма будет незначительной потерей. С другой стороны – при доходности в 90% даже такое минимальное капиталовложения можно очень быстро увеличить.
- У брокера Binomo для торговли предлагается одна из лучших на рынке торговых платформ, которая оснащена профессиональным инструментарием для анализа рынка.
- Научиться торговать у брокера можно с помощью демо-счета и суммы виртуальных средств, то есть, понять принцип торговли бинарными опционами и увидеть реальный потенциал опционной торговли можно и без пополнения реального торгового счета.
- Брокер Биномо обеспечивает своих клиентов качественным бесплатным обучением, с помощью которого даже «чайник» сможет стать успешным трейдером. Кроме того, в компании предлагается профессиональная аналитическая поддержка с ежедневными новостными обзорами, техническим анализом и инвестиционными идеями, что существенно упрощает торговлю.
- Binomo – это регулируемый брокер, то есть, деятельность компании контролируется специализированной организацией ЦРОФР. Плюс, все средства клиентов застрахованы в компенсационном фонде данного регулятора от банкротства брокера.
- Ввести заработанные средства у брокера можно в течении 24 часов.
Таким образом, у нас есть все основания назвать брокера Binomo одной из самых интересных и выгодных компаний на рынке брокерских услуг. Поэтому, перейдем к основному вопросу относительно бинарных опционов, и рассмотрим ряд влияющих на успех факторов.
Торговая система для бинарных опционов
Несмотря на простой алгоритм бинарных опционов, в торговле обязателен системный подход. По сути, только торговая система для бинарных опционов в комплексе с правильным управлением оборотными средствами способна обеспечить реальный заработок с помощью данного финансового инструмента.
По сути, только торговая система для бинарных опционов в комплексе с правильным управлением оборотными средствами способна обеспечить реальный заработок с помощью данного финансового инструмента.
Чтобы продемонстрировать вам принцип заработка на торговом терминале Binomo, мы выбрали самую простую торговую стратегию. Эта стратегия построена на основе двух технических индикаторов – Скользящее среднее и Волны Боллинджера.
Для применения данной системы необходимо:
- Установить на график вышеуказанные индикаторы из специализированного набора платформы, при этом, для Скользящего среднего нужно установить дополнительные настройки – период 1 и тип построения Weighted.
- Для заключения сделки с определенным прогнозом, необходимо определить комплексный торговых сигнал от индикаторов, который отобразится касанием или небольшим выходом скользящей средней и котировок актива за рамки канала Боллинджера. Прогноз движения цены необходимо устанавливать во внутрь канала.
Вот как вышеописанный сигнал будет выглядеть на графике котировок платформы Binomo:
С помощью вышеописанной торговой системы для бинарных опционов можно закрывать прибыльным результатом более 80% заключаемых сделок. Это значит, что с учетом высокой доходности опционов и короткого срока экспирации, можно всего за неделю увеличить свой стартовый капитал в несколько раз!
Таким образом, сомневаться в том, реально ли заработать на бинарных опционах, нет причин. Бинарные опционы однозначно способны обеспечить высокий уровень дохода!
Отзывы
Андрей, г.Тверь, 26-02-2016
Хочу оставить свой отзыв, чтобы развеять сомнения сомневающимся. Действительно реальный способ заработать. Сначала долго сомневался и я, но потом решил все-таки рискнуть. Сначала вложил 10 долларов, которые за неделю разогнал до 80 долларов. Начинал и сейчас торгую у Биномо – нормальный брокер. Кстати, благодаря его демо-платформе и научился торговать.
Татьяна, г.Москва, 18-03-2016
Бинарными опционами заинтересовалась еще год назад. Тогда попалась реклама о бесплатных опционах, которые предлагались у Биномо – можно было начать торговать на деньги брокера. Конечно же, воспользовалась этой возможностью и сегодня не жалею, что выбрала именно этого брокера.
Олег, г.Санкт-Петербург, 29-03-2016
БО – теперь мой основной источник дохода! Раньше работал на государство и получал копейки, от безысходности искал дополнительный заработок и нашел бинарные опционы. Повезло, что зарегистрировался сразу у Биномо (потом узнал, что на этом рынке полно мошенников) – тут реально позволяют зарабатывать.
Людмила, г.Москва, 12-06-2016
Не смогла удержаться от комментария. Хочу подчеркнуть, Биномо – хороший брокер. Начинала торговать у другого брокера и сначала разочаровалась в бинарных опционах. Потом решила попробовать в другой компании – у Биномо, и поняла, почему у меня не получалось зарабатывать. Все дело в торговой платформе – у Биномо она профессиональная, поэтому и торговать на ней намного проще, чем на отсталых платформах других брокеров.
Элина, г.Краснодар, 29-08-2016
Мое рабочее место теперь дома – ушла со старой работы и теперь торгую бинарными опционам, чем полностью себя обеспечиваю. Брокера выбирала очень долго, попадались то мошенники, то компании с драконовскими торговыми условиями. Наконец-то нашла Биномо — кроме выгодных торговых условий этот брокер предлагает качественные сервисы.
Сколько можно заработать на Binomo? — Binomo (Биномо) – отзывы, стратегии, вход
По сути название этой небольшой заметки включает в себя два часто задаваемых вопроса. Для тех кто только встал на увлекательны трейдерский путь работы с бинарными опционами эти вопросы особенно актуальны. Любой человек хочет знать сколько он будет зарабатывать, выполняя ту или иную деятельность. Торговля бинарными опционами не является исключением. С другой стороны заработок здесь находиться в зависимости от многих факторов. Одним из основных является грамотный выбор актива, о котором пойдет речь ниже.
Одним из основных является грамотный выбор актива, о котором пойдет речь ниже.
Делаем правильный выбор активов на площадке Binomo
Одним из самых весомых преимуществ площадки Binomo является многообразие активов. Каждый трейдер сможет найти здесь, что-то для себя. Конечно, важно понимать, что одни активы применяются под одни стратегии, вторые совершенно под другие. Некоторые трейдеры попросту начинают теряться в многообразии вариантов.
Именно поэтому мы бы хотели дать вам простой, но эффективный совет. При использовании бинарных стратегий на базе поведения тренда нужно делать выбор в пользу валютных пар, обладающих волатильностью. Для этого прекрасно подходят активы GBP/JPY, EUR/USD, EUR/JPY, GBP/USD. Отношения этих валют находятся в тренде большие временные интервалы, а значит их поведение более предсказуемо.
Любителям канального трейдинга лучше использовать не слишком подвижные валюты, так как время операций здесь короче. Применяйте NZD/USD, USD/CHF, EUR/GBP, AUD/USD. Преимущественной плавностью в канале также обладают акции таких корпораций как APPLE и GOOGLE.
Масштабы заработка на платформе Биномо
На самом деле, то сколько вы будете зарабатывать зависит от вашего подхода к торговле. Есть такое правило, чем большими суммами вы оперируете, тем больше денег вы можете заработать. Однако оно верно только для подготовленных игроков, которые могут правильно оценивать риски. Начинающий трейдер без определенной подготовки может попросту слить депозит. Именно поэтому мы рекомендуем не гнаться за большими деньгами на начальном этапе. Открывайте сделки на суммы, не превышающие 10% от вашего счета. Именно так вы наберете необходимый «скилл» и сохраните свой депозит. Стоит также отметить, что даже на минимальных ставках (на Binomo это 10 долл.) вы сможете прилично заработать, просто необходимо открывать больше сделок.
Просмотрите последнею топовую таблицу трейдеров Биномо:
Работа с минимальными ставками хороша и в плане тестирования стратегий. Да в поисках рабочей стратегии для бинарных опционов вы будете терять деньги, но такие потери будут минимальными. Кроме этого Binomo предоставляет подарочные сделки, которые также хороши для тестирования. Постепенно вы найдете то, что подойдет именно вам. Как правило, с этого и начинается эффективный, прибыльный заработок!
Да в поисках рабочей стратегии для бинарных опционов вы будете терять деньги, но такие потери будут минимальными. Кроме этого Binomo предоставляет подарочные сделки, которые также хороши для тестирования. Постепенно вы найдете то, что подойдет именно вам. Как правило, с этого и начинается эффективный, прибыльный заработок!
Зарабатывайте столько, сколько пожелаете вместе с Binomo!
Читайте на сайте:
Регистрация и вход на сайт Binomo (Биномо)
Акции бинарных опционов у брокера Binomo
Открытие демо счета на сайте Биномо
Как заработать на Binomo без вложений
Можно ли зарабатывать на Binomo без вложения реальных денег — этот вопрос интересует основную массу потенциальных онлайн трейдеров, которые рассматривают в качестве торговой платформы сервис этого брокера. Мы предлагаем вам стратегию и рекомендации как зарабатывать на Биномо без собственного стартового капитала.
Начнем с главного: чтобы зарабатывать на бинарном трейдинге реальные деньги, инвестору просто необходим инвестиционный капитал. Binomo в данном вопросе предлагает самый привлекательный выход для инвесторов, если они не располагают собственными средствами.
Речь идет о демо-счете, который оператор открывает клиентам без необходимости вложения денег. При работе в демо режиме трейдеры могут принять участие в турнире, который компания проводит на постоянной основе.
Призовой фонд составляет 150 долларов, причем выплачивается реальными средствами, которые можно в дальнейшем вложить в трейдинг или монетизировать на банковскую карту.
Для выигрыша участнику торговли необходимо всего лишь достичь наилучших показателей торговли в течение недели. Таким образом новички получают реальную возможность начать трейдинг без собственного капитала, а профессионалы могут заработать на своем опыте и знаниях.
Инструменты для торговли по стратегии без вложений
В вопросе как заработать на Binomo без вложений мы разобрались, перейдем к технической стороне и в частности к стратегии, которая поможет получить главный приз турнира.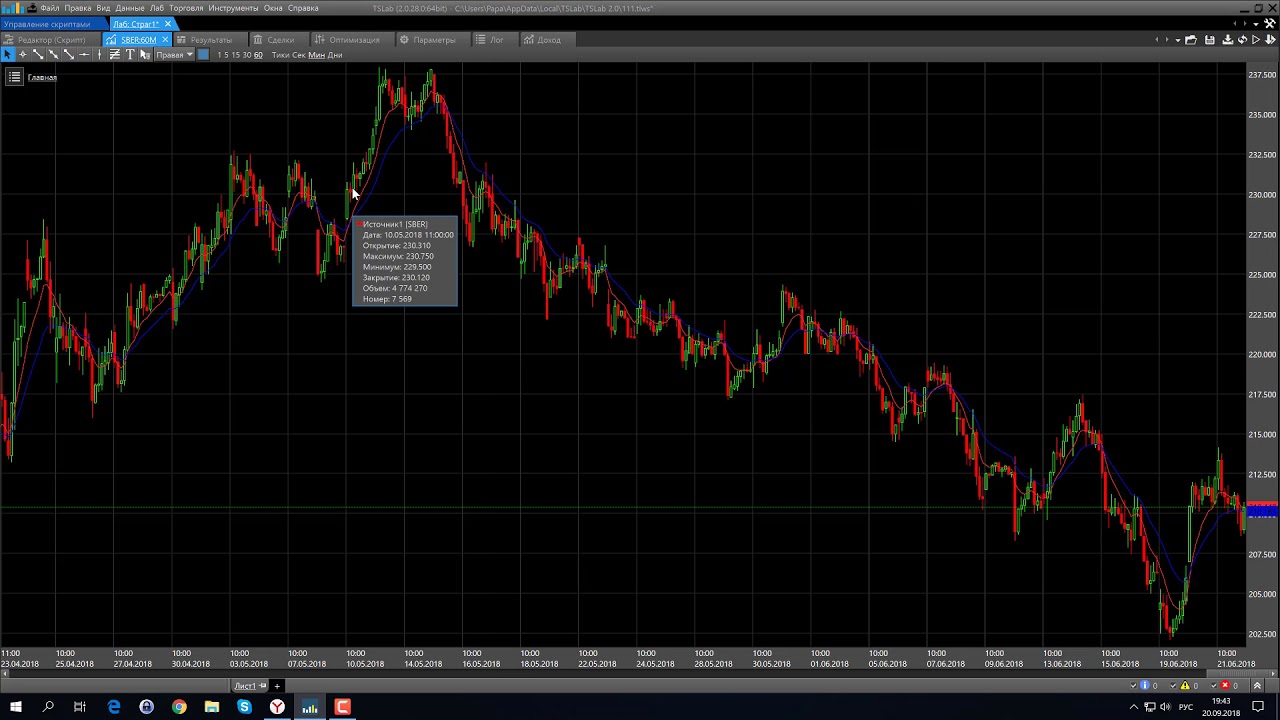 Наша задача получить максимально возможный результат в достаточно короткий период времени, поэтому для трейдинга нам понадобятся опционы с минимальным сроком истечения.
Наша задача получить максимально возможный результат в достаточно короткий период времени, поэтому для трейдинга нам понадобятся опционы с минимальным сроком истечения.
В связи с этим мы сможем оформлять больше контрактов и быстрее получим прибыль. В качестве оптимального вида контрактов предлагаем использовать турбоопционы с периодичностью истечения от 2 до 5 минут. Несмотря на то, что мы будем использовать в трейдинге виртуальные средства, и наши финансовые риски будут носить только виртуальный характер, конечный результат будет вполне реальным и для его достижения нам потребуется стратегия с максимальным уровнем эффективности сигналов.
В качестве самого простого и прибыльного приема торговли предлагаем систему, основанную на уровнях тренда. Здесь используется закономерность построения котировок относительно цены актива. Если внимательно изучить котировки, можно заметить, что при достижении определенных показателей цена актива проводит развороты, формируя при этом максимумы и минимумы. Именно экстремумы рынка мы будем использовать для определения уровней тренда – поддержки и сопротивления.
Для этого потребуется графический сервис «Канал», который предлагается на терминале Binomo. С его помощью необходимо соединить ближайшие экстремумы текущего тренда, в результате мы получим уровни поддержки или сопротивления, при достижении которых будем оформлять торговые контракты:
Так как нам необходим быстрый и максимально большой результат, мы будем работать сразу в двух направлениях движения рынка. Для увеличения динамики торговых операций используйте краткосрочный таймфрейм рабочего графика – оптимально 30 секунд. В таком режиме существенно увеличивается количество сигналов.
Активы
В этом вопросе на первый план выходят два показателя – уровни выплат, которые предлагаются по определенному базовому активу и показатели волатильности инструмента. Для использования нашей стратегии торговли на Биномо без вложения денег, мы рекомендуем в качестве торговых активов — основные валютные пары. На этих инструментах брокер предлагает контракты с прибыльностью до 90%, что поможет нам в быстром увеличении капитала.
На этих инструментах брокер предлагает контракты с прибыльностью до 90%, что поможет нам в быстром увеличении капитала.
Как торговать?
В данном варианте технической стратегии сигналами для оформления бинарных контрактов, выступают моменты разворотов цены от уровней тренда:
- Опционы CALL открываем при касании котировками уровня поддержки;
- Сделки PUT используем в трейдинге при развороте цены от уровня сопротивления.
Таким образом при работе на 30-ти секундном таймфрейме графика котировок мы можем получить до 25 сигналов для оформления опционов, 65-90% из которых дадут прибыль.
Минусы
Система, несмотря на высокую эффективность, дает сбои в моменты импульсного увеличения волатильности котировок, которые происходят в результате выхода важной макроэкономической статистики. Чтобы не получить убытки, в такой момент от трейдинга лучше отказаться.
Плюсы
Кроме основного преимущества – заработок реальных средств без вложений, стратегия предлагает целый ряд положительных моментов, которые можно в последствии использовать в торговле на реальных деньгах: высокий уровень торговой динамики, максимальная эффективность сигналов, хорошие показатели общего результата трейдинга.
В итоге, мы можем четко сказать, что стратегия торговли на Биномо без вложения денег существует и она реально работает. При использовании системы на демо-счете вы можете рассчитывать на призовое место в турнире и получение средств для стартового капитала.
Плюсы
- Для любого уровня трейдеров
- До 25 опционов в час
- Прибыльных сделок от 65%
- Простые правила
Минусы
- Не для торговли по новостям
Основы биномиального распределения
Даже если вы не знаете биномиальное распределение по имени и никогда не посещали углубленные курсы статистики в колледже, вы от природы это понимаете. На самом деле, да. Это способ оценки вероятности того, что дискретное событие произойдет или не произойдет. И у него есть множество приложений в области финансов. Вот как это работает:
На самом деле, да. Это способ оценки вероятности того, что дискретное событие произойдет или не произойдет. И у него есть множество приложений в области финансов. Вот как это работает:
Вы начинаете с попытки сделать что-нибудь — подбрасывание монеты, штрафные броски, вращение колеса рулетки, что угодно. Единственное условие — то, о чем идет речь, должно иметь ровно два возможных результата.Успех или неудача, вот и все. (Да, колесо рулетки имеет 38 возможных исходов. Но с точки зрения игрока, делающего ставки, их всего два. Вы либо выиграете, либо проиграете.)
В нашем примере мы будем использовать штрафные броски, потому что они немного интереснее точной и неизменной 50% вероятности выпадения орла на монету. Допустим, вы Дирк Новицки из Dallas Mavericks, который выполнил 89,8% штрафных бросков в сезоне 2017–2018 гг. Для наших целей мы назовем это 90%. Если бы вы поставили его под удар прямо сейчас, каковы были бы шансы, что он попадет (по крайней мере) в девять из 10?
Нет, не на 100%.И не 90%.
Их 74%, хотите верьте, хотите нет. Вот формула. Мы все здесь взрослые, не надо бояться экспонентов и греческих букв:
n — количество попыток. В этом случае 10.
i — это количество успехов, равное девяти или 10. Мы вычислим вероятность для каждого, а затем сложим их.
p — вероятность успеха каждого отдельного события, равная 0,9.
Шанс достижения цели, т.е.{n-i} \ end {выровнен}
Я = 0∑k (ni) pi (1 − p) n − i
Лечебная математическая нотация, если вам нужно разбить термины в этом выражении дальше:
Взаимодействие с другими людьми
(
п
я
)
знак равно
п
!
(
п
—
я
)
!
я
!
\ begin {align} & \ left (\ begin {matrix} n \\ i \ end {matrix} \ right) = \ frac {n!} {(n-i)! i!} \ end {выравнивается}
(НИ) = (П-Я)! Я! П!
Это «биномиальное» в биномиальном распределении: то есть два члена. Нас интересует не только количество успехов или попыток, но и то, и другое. Одно без другого для нас бесполезно.
Одно без другого для нас бесполезно.
Дополнительные математические обозначения:! является факториалом: умножение положительного целого числа на каждое меньшее положительное целое число. Например,
Взаимодействие с другими людьми
5
!
знак равно
5
×
4
×
3
×
2
5! = 5 \ \ раз \ 4 \ \ раз \ 3 \ раз \ 2
5! = 5 × 4 × 3 × 2
Подставьте числа, помня, что нам нужно решить как 9 из 10 штрафных бросков, так и 10 из 10, и мы получим
Взаимодействие с другими людьми
(
1
0
!
9
!
1
!
×
.
9
.
9
×
.
1
.0 \ вправо)
(9! 1! 10! × 0,9,9 × .1,1) + (10! 10! × 0,91 × 0,10)
= 0,387420489 (вероятность выпадения девяти) + 0,3486784401 (шанс выпадения всех десяти)
= 0,736098929
Это кумулятивное распределение , в отличие от простого распределения вероятности . Кумулятивное распределение — это сумма нескольких распределений вероятностей (в нашем случае это было бы два). Кумулятивное распределение вычисляет вероятность попадания в диапазон значений — здесь девять или 10 из 10 штрафных бросков — вместо одного ценить.Когда мы спрашиваем, каковы шансы Новицки забить девять из 10, следует понимать, что мы имеем в виду «девять или лучше из 10», а не «ровно девять из 10».
Если вы хотите вычислить функцию биномиального распределения для определенной серии событий, вам не нужно рассчитывать ее самостоятельно. У сотрудников Stat Trek есть биномиальный калькулятор, который сделает всю работу за вас. Все, что вам нужно сделать, это указать значения n , i и p .
Так при чем здесь финансы? Больше, чем вы думаете.Допустим, вы банк, кредитор, который с точностью до трех десятичных знаков знает вероятность дефолта конкретного заемщика. Каковы шансы того, что так много заемщиков неплатежеспособны, что они сделают банк неплатежеспособным? После того, как вы воспользуетесь функцией кумулятивного биномиального распределения для вычисления этого числа, у вас будет лучшее представление о том, как оценивать страхование и, в конечном итоге, сколько денег предоставить в долг и сколько оставить в резерве.
Вы когда-нибудь задумывались, как определяются начальные цены опционов? То же самое, вроде того.Если волатильная базовая акция имеет шанс p достичь определенной цены, вы можете посмотреть, как акция движется в течение ряда периодов n , чтобы определить, по какой цене опционы должны продаваться.
Применение функции биномиального распределения к финансам дает некоторые удивительные, если не полностью противоречащие интуиции, результаты; примерно так же, как вероятность того, что игрок, выполняющий штрафные броски с 90% штрафных бросков, выполнит 90% своих штрафных бросков, составляет менее 90%. Предположим, у вас есть ценная бумага, которая имеет столько же шансов на 20% -ную прибыль, так и на 20% -ную потерю.Если цена ценной бумаги упадет на 20%, каковы шансы, что она вернется к исходному уровню? Помните, что простой соответствующий прирост в 20% не снизит его: акция, которая упала на 20%, а затем выросла на 20%, все равно упадет на 4%. Продолжайте чередовать 20% падения и роста, и в конечном итоге акции обесценятся.
Итог
Аналитики, разбирающиеся в биномиальном распределении, имеют под рукой дополнительный набор качественных инструментов для определения цен, оценки риска и избежания неприятных результатов, которые могут возникнуть в результате недостаточной подготовки.Когда вы поймете биномиальное распределение и его часто удивительные результаты, вы значительно опередите массы.
Понимание модели ценообразования биномиальных опционов
Определение цен на акции
Сложно договориться о точных ценах на любой торгуемый актив, поэтому цены на акции постоянно меняются. В действительности компании практически не меняют свои оценки на ежедневной основе, но их стоимость акций и оценки меняются почти каждую секунду. Эта сложность достижения консенсуса в отношении правильной цены на любой торгуемый актив приводит к краткосрочным возможностям арбитража.
Но в большинстве случаев успешное инвестирование сводится к простому вопросу современной оценки — какова правильная текущая цена сегодня для ожидаемой будущей выплаты?
Оценка биномиальных опционов
На конкурентном рынке, чтобы избежать возможностей арбитража, активы с идентичной структурой выплат должны иметь одинаковую цену. Оценка опционов была сложной задачей, и колебания цен открывают возможности для арбитража. Модель Блэка-Шоулза остается одной из самых популярных моделей, используемых для определения цен, но имеет ограничения.Взаимодействие с другими людьми
Модель ценообразования биномиальных опционов — еще один популярный метод, используемый для определения цен.
Примеры
Предположим, есть опцион колл на конкретную акцию с текущей рыночной ценой 100 долларов. Страйк-цена опциона «при деньгах» (ATM) составляет 100 долларов США со сроком действия до одного года. Есть два трейдера, Питер и Паула, которые оба согласны с тем, что цена акций вырастет либо до 110 долларов, либо упадет до 90 долларов через год.
Они согласны с ожидаемыми уровнями цен в заданный период времени в один год, но не согласны с вероятностью движения вверх или вниз.Питер считает, что вероятность того, что цена акции вырастет до 110 долларов, составляет 60%, а Паула — 40%.
Исходя из этого, кто будет готов заплатить больше за опцион колл? Возможно, Питер, так как он ожидает высокой вероятности движения вверх.
Расчет биномиальных опционов
Два актива, от которых зависит оценка, — это колл-опцион и базовая акция. Между участниками существует договоренность о том, что цена базовой акции может измениться с текущих 100 долларов до 110 или 90 долларов в течение одного года, и никакие другие изменения цены невозможны.
В мире без арбитража, если вам нужно создать портфель, состоящий из этих двух активов, опциона колл и базовых акций, так что независимо от того, где идет базовая цена — 110 или 90 долларов — чистая прибыль от портфеля всегда остается неизменной. . Предположим, вы покупаете d акций базового актива и короткие опционы колл для создания этого портфеля.
Если цена упадет до 110 долларов, ваши акции будут стоить 110 долларов в день, и вы потеряете 10 долларов на выплате короткого колла. Чистая стоимость вашего портфеля будет (110d — 10).
Если цена упадет до 90 долларов, ваши акции будут стоить 90 долларов в день, и срок действия опциона будет бесполезным. Чистая стоимость вашего портфеля будет (90d).
Если вы хотите, чтобы стоимость вашего портфеля оставалась неизменной независимо от того, где находится базовая цена акций, тогда стоимость вашего портфеля должна оставаться неизменной в любом случае:
Взаимодействие с другими людьми
час
(
d
)
—
м
знак равно
л
(
d
)
куда:
час
знак равно
Наивысшая потенциальная базовая цена
d
знак равно
Количество базовых акций
м
знак равно
Деньги, потерянные при выплате короткого звонка
л
знак равно
Самая низкая потенциальная базовая цена
\ begin {align} & h (d) — m = l (d) \\ & \ textbf {где:} \\ & h = \ text {Наивысшая потенциальная цена базового актива} \\ & d = \ text {Количество базовых акций} \ \ & m = \ text {Деньги, потерянные при выплате короткого колла} \\ & l = \ text {Самая низкая потенциальная базовая цена} \\ \ end {выровнено}
H (d) −m = l (d) где: h = Наивысшая потенциальная цена базового актива = Количество базовых акций m = Деньги, потерянные при коротком колл payoffl = Самая низкая потенциальная цена базового актива
Таким образом, если вы покупаете половину акции, предполагая, что дробные покупки возможны, вам удастся создать портфель, так что его стоимость останется одинаковой в обоих возможных состояниях в течение заданного периода времени в один год.
Взаимодействие с другими людьми
1
1
0
d
—
1
0
знак равно
9
0
d
d
знак равно
1
2
\ begin {align} & 110d — 10 = 90d \\ & d = \ frac {1} {2} \\ \ end {align}
110d − 10 = 90dd = 21
Стоимость этого портфеля, обозначенная (90d) или (110d — 10) = 45, равна одному году назад. Чтобы рассчитать ее приведенную стоимость, ее можно дисконтировать с помощью безрисковой нормы прибыли (при условии, что 5%).
Взаимодействие с другими людьми
Приведенная стоимость
знак равно
9
0
d
×
е
(
—
5
%
×
1
Год
)
знак равно
4
5
×
0
. {(-5 \% \ times 1 \ text {Year})} \\ & = 45 \ times 0.9523 \\ & = 42,85 \\ \ end {выровнено}
Текущая стоимость = 90d × e (−5% × 1 год) = 45 × 0,9523 = 42,85
Поскольку в настоящее время портфель состоит из ½ доли базовых акций (с рыночной ценой 100 долларов США) и одного короткого колл-колла, он должен быть равен приведенной стоимости.
Взаимодействие с другими людьми
1
2
×
1
0
0
—
1
×
Стоимость звонка
знак равно
$
4
2
.
8
5
Стоимость звонка
знак равно
$
7
.
1
4
, То есть цена звонка на сегодня
\ begin {align} & \ frac {1} {2} \ times 100 — 1 \ times \ text {Цена звонка} = \ 42,85 $ \\ & \ text {Цена звонка} = \ 7 $.14 \ text {, то есть цена звонка на сегодня} \\ \ end {выравнивается}
21 × 100−1 × Цена звонка = 42,85 $ Цена звонка = 7,14 $, то есть цена звонка на сегодня
Поскольку это основано на предположении, что стоимость портфеля остается неизменной независимо от того, в каком направлении идет базовая цена, вероятность движения вверх или вниз не играет никакой роли. Портфель остается безрисковым независимо от движений базовой цены.
В обоих случаях (предполагается, что при повышении до 110 долл. США и при понижении до 90 долл.) Ваш портфель нейтрален по отношению к риску и приносит безрисковую норму прибыли.
Следовательно, оба трейдера, Питер и Паула, были бы готовы заплатить одинаковые 7,14 доллара за этот опцион колл, несмотря на различное восприятие вероятностей восходящих движений (60% и 40%). Их индивидуально воспринимаемые вероятности не имеют значения при оценке опционов.
Предположим вместо этого, что индивидуальные вероятности имеют значение, возможно, представились возможности арбитража. В реальном мире такие возможности арбитража существуют с незначительной разницей в цене и исчезают в краткосрочной перспективе.
Но где же столь разрекламированная волатильность всех этих расчетов, важный и чувствительный фактор, влияющий на ценообразование опционов?
Неустойчивость уже включена в характер определения проблемы. Предполагая два (и только два — отсюда и название «биномиальные») состояния уровней цен (110 и 90 долларов), волатильность подразумевается в этом предположении и включается автоматически (10% в любом случае в этом примере).
Блэк-Скоулз
Но является ли этот подход правильным и согласуется ли с общепринятым ценообразованием Блэка-Шоулза? Результаты калькулятора опционов (любезно предоставленные OIC) полностью совпадают с вычисленным значением:
К сожалению, реальный мир не так прост, как «всего два состояния».«Акция может достичь нескольких ценовых уровней до истечения срока.
Можно ли включить все эти несколько уровней в биномиальную модель ценообразования, которая ограничена только двумя уровнями? Да, это очень возможно, но чтобы понять это, нужна простая математика.
Простая математика
Чтобы обобщить эту проблему и ее решение:
«X» — это текущая рыночная цена акции, а «X * u» и «X * d» — будущие цены для движений вверх и вниз «t» лет спустя.Фактор «u» будет больше единицы, поскольку он указывает на движение вверх, а «d» будет находиться между нулем и единицей. В приведенном выше примере u = 1,1 и d = 0,9.
Выплаты по опционам колл составляют «P до » и «P dn » для движений вверх и вниз в момент истечения срока.
Изображение Сабрины Цзян © Investopedia 2020
Если вы создадите портфель из акций «s», приобретенных сегодня, и продадите один опцион колл, то по истечении времени «t»:
Взаимодействие с другими людьми
ВУМ
знак равно
s
×
Икс
×
ты
—
п
вверх
куда:
ВУМ
знак равно
Стоимость портфеля при движении вверх
\ begin {align} & \ text {VUM} = s \ times X \ times u — P_ \ text {up} \\ & \ textbf {где:} \\ & \ text {VUM} = \ text {Стоимость портфеля в случае движения вверх} \\ \ end {выравнивается}
VUM = s × X × u − Pup, где: VUM = Стоимость портфеля в случае движения вверх
Взаимодействие с другими людьми
VDM
знак равно
s
×
Икс
×
d
—
п
вниз
куда:
VDM
знак равно
Стоимость портфеля при движении вниз
\ begin {align} & \ text {VDM} = s \ times X \ times d — P_ \ text {down} \\ & \ textbf {где:} \\ & \ text {VDM} = \ text {Стоимость портфеля в случае движения вниз} \\ \ end {выравнивается}
VDM = s × X × d − Pdown, где: VDM = Стоимость портфеля в случае нисходящего движения
Для аналогичной оценки в любом случае движения цены:
Взаимодействие с другими людьми
s
×
Икс
×
ты
—
п
вверх
знак равно
s
×
Икс
×
d
—
п
вниз
s \ times X \ times u — P_ \ text {вверх} = s \ times X \ times d — P_ \ text {down}
s × X × u − Pup = s × X × d − Pdown
Взаимодействие с другими людьми
s
знак равно
п
вверх
—
п
вниз
Икс
×
(
ты
—
d
)
знак равно
Количество акций для покупки
знак равно
безрисковый портфель
\ begin {align} s & = \ frac {P_ \ text {up} — P_ \ text {down}} {X \ times (u — d)} \\ & = \ text {Количество акций для покупки} \\ & \ phantom {=} \ text {безрисковый портфель} \\ \ end {выровнен}
s = X × (u − d) Pup −Pdown = количество акций для покупки = безрисковый портфель
Будущая стоимость портфеля на конец «t» лет будет:
Взаимодействие с другими людьми
В случае движения вверх
знак равно
s
×
Икс
×
ты
—
п
вверх
знак равно
п
вверх
—
п
вниз
ты
—
d
×
ты
—
п
вверх
\ begin {align} \ text {В случае перемещения вверх} & = s \ times X \ times u — P_ \ text {up} \\ & = \ frac {P_ \ text {up} — P_ \ text {down} } {u — d} \ times u — P_ \ text {up} \\ \ end {выровнено}
В случае движения вверх = s × X × u − Pup = u − dPup −Pdown × u − Pup
Взаимодействие с другими людьми
В случае движения вниз
знак равно
s
×
Икс
×
d
—
п
вниз
знак равно
п
вверх
—
п
вниз
ты
—
d
×
d
—
п
вниз
\ begin {align} \ text {В случае перемещения вниз} & = s \ times X \ times d — P_ \ text {down} \\ & = \ frac {P_ \ text {up} — P_ \ text {down} } {u — d} \ times d — P_ \ text {down} \\ \ end {выровнено}
В случае движения вниз = s × X × d − Pdown = u − dPup −Pdown × d − Pdown
Текущая стоимость может быть получена путем дисконтирования с безрисковой нормой доходности:
Взаимодействие с другими людьми
PV
знак равно
е
(
—
р
т
)
×
[
п
вверх
—
п
вниз
ты
—
d
×
ты
—
п
вверх
]
куда:
PV
знак равно
Текущая стоимость
р
знак равно
Норма прибыли
т
знак равно
Время в годах
\ begin {align} & \ text {PV} = e (-rt) \ times \ left [\ frac {P_ \ text {up} — P_ \ text {down}} {u — d} \ times u — P_ \ text {вверх} \ right] \\ & \ textbf {где:} \\ & \ text {PV} = \ text {Текущая стоимость} \\ & r = \ text {Норма прибыли} \\ & t = \ text {Время в годах} \\ \ end {выровнено}
PV = e (−rt) × [u − dPup −Pdown × u − Pup], где: PV = Текущий оценщик = Скорость возврата = Время в годах
Это должно соответствовать портфелю акций «s» по цене X, а стоимость короткого колл «c» (текущее владение (s * X — c) должно соответствовать этому расчету.) Решение для «c», наконец, дает это как:
Примечание. Если премия за колл сокращена, это должно быть добавление к портфелю, а не вычитание.
Взаимодействие с другими людьми
c
знак равно
е
(
—
р
т
)
ты
—
d
×
[
(
е
(
—
р
т
)
—
d
)
×
п
вверх
+
(
ты
—
е
(
—
р
т
)
)
×
п
вниз
]
c = \ frac {e (-rt)} {u — d} \ times [(e (-rt) — d) \ times P_ \ text {up} + (u — e (-rt)) \ times P_ \ текст {вниз}]
c = u − de (−rt) × [(e (−rt) −d) × Pup + (u − e (−rt)) × Pdown]
Другой способ написать уравнение — переставить его:
Принимая «q» как:
Взаимодействие с другими людьми
q
знак равно
е
(
—
р
т
)
—
d
ты
—
d
q = \ frac {e (-rt) — d} {u — d}
q = u − de (−rt) −d
Тогда уравнение принимает следующий вид:
Взаимодействие с другими людьми
c
знак равно
е
(
—
р
т
)
×
(
q
×
п
вверх
+
(
1
—
q
)
×
п
вниз
)
c = e (-rt) \ times (q \ times P_ \ text {вверх} + (1 — q) \ times P_ \ text {down})
c = e (−rt) × (q × Pup + (1 − q) × Pdown)
Преобразование уравнения в «q» открыло новую перспективу.
Теперь вы можете интерпретировать «q» как вероятность восходящего движения базового актива (поскольку «q» связано с P до , а «1-q» связано с P dn ). В целом, уравнение представляет собой текущую цену опциона, дисконтированную стоимость его выплаты по истечении срока.
Этот «Q» отличается от
Чем эта вероятность «q» отличается от вероятности движения вверх или вниз базового актива?
Взаимодействие с другими людьми
ВСП
знак равно
q
×
Икс
×
ты
+
(
1
—
q
)
×
Икс
×
d
куда:
ВСП
знак равно
Стоимость акций во время
т
\ begin {align} & \ text {VSP} = q \ times X \ times u + (1 — q) \ times X \ times d \\ & \ textbf {где:} \\ & \ text {VSP} = \ text {Значение цены акции на момент времени} t \\ \ end {выровнено}
VSP = q × X × u + (1 − q) × X × d, где: VSP = стоимость акций в момент времени t
Подставив значение «q» и переставив, цена акции в момент «t» составит:
Взаимодействие с другими людьми
Стоимость акций
знак равно
е
(
р
т
)
×
Икс
\ begin {выровнен} & \ text {курс акций} = e (rt) \ times X \\ \ end {выровнен}
Цена акции = e (rt) × X
В этом предполагаемом мире двух государств цена акций просто растет на безрисковую норму прибыли, точно так же, как безрисковый актив, и, следовательно, остается независимой от любого риска.Инвесторы безразличны к риску в рамках этой модели, поэтому она представляет собой нейтральную к риску модель.
Вероятности «q» и «(1-q)» известны как вероятности, нейтральные к риску, а метод оценки известен как модель оценки, нейтральная к риску.
В примере сценария есть одно важное требование — структура будущих выплат должна быть точной (уровень 110 и 90 долларов). В реальной жизни такая ясность в отношении ступенчатых уровней цен невозможна; цена скорее движется случайным образом и может колебаться на нескольких уровнях.
Чтобы расширить пример, предположим, что возможны двухступенчатые уровни цен. Мы знаем окончательные выплаты на втором этапе, и нам нужно оценить опцион сегодня (на начальном этапе):
Изображение Сабрины Цзян © Investopedia 2020
Работая в обратном направлении, промежуточная оценка на первом этапе (при t = 1) может быть выполнена с использованием окончательных выплат на втором этапе (t = 2), а затем, используя эти рассчитанные оценки первого этапа (t = 1), современная оценка (t = 0) может быть достигнуто с помощью этих расчетов.
Чтобы получить цену опциона под номером два, используются выплаты по ставке четыре и пять. Для получения цены на номер три используются выплаты в размере пять и шесть. Наконец, рассчитанные выплаты по двум и трем числам используются для получения цены номер один.
Обратите внимание, что этот пример предполагает одинаковый коэффициент для движений вверх (и вниз) на обоих шагах — u и d применяются комбинированным образом.
Рабочий пример
Предположим, что опцион пут с ценой исполнения 110 долларов в настоящее время торгуется по 100 долларов и истекает через год.Годовая безрисковая ставка — 5%. Ожидается, что цена будет увеличиваться на 20% и снижаться на 15% каждые шесть месяцев.
Здесь u = 1,2 и d = 0,85, x = 100, t = 0,5.
используя полученную выше формулу
Взаимодействие с другими людьми
q
знак равно
е
(
—
р
т
)
—
d
ты
—
d
q = \ frac {e (-rt) — d} {u — d}
q = u − de (−rt) −d
получаем q = 0,35802832
стоимость опциона пут в точке 2,
Взаимодействие с другими людьми
п
2
знак равно
е
(
—
р
т
)
×
(
п
×
п
вверх вверх
+
(
1
—
q
)
п
UPDN
)
куда:
п
знак равно
Цена оферты
\ begin {align} & p_2 = e (-rt) \ times (p \ times P_ \ text {upup} + (1 — q) P_ \ text {updn}) \\ & \ textbf {где:} \\ & p = \ text {Цена оферты} \\ \ end {выравнивается}
P2 = e (−rt) × (p × Pupup + (1 − q) Pupdn), где: p = цена опциона пут
При условии P upup андерлаинг будет = 100 * 1.2 * 1,2 = 144 доллара до P вверх до = ноль
При условии P updn базовый актив будет = 100 * 1,2 * 0,85 = 102 доллара, что приведет к P updn = 8 долларов
При условии P dndn базовый актив будет = 100 * 0,85 * 0,85 = 72,25 доллара, что приведет к P dndn = 37,75 доллара
p 2 = 0,975309912 * (0,35802832 * 0 + (1-0,35802832) * 8) = 5,008970741
Аналогично, p 3 = 0,975309912 * (0,35802832 * 8 + (1-0,35802832) * 37,75) = 26.42958924
Взаимодействие с другими людьми
п
1
знак равно
е
(
—
р
т
)
×
(
q
×
п
2
+
(
1
—
q
)
п
3
)
p_1 = e (-rt) \ times (q \ times p_2 + (1 — q) p_3)
p1 = e (−rt) × (q × p2 + (1 − q) p3)
Следовательно, стоимость опциона пут p 1 = 0,975309912 * (0,35802832 * 5,008970741 + (1-0,35802832) * 26,42958924) = 18,29 доллара США.
Точно так же биномиальные модели позволяют разбить всю длительность опциона на несколько дополнительных шагов и уровней. Используя компьютерные программы или электронные таблицы, вы можете двигаться в обратном направлении на один шаг за раз, чтобы получить текущую стоимость желаемого варианта.
Другой пример
Предположим, что опцион пут европейского типа с девятью месяцами до истечения срока действия, страйк-ценой 12 долларов и текущей базовой ценой 10 долларов. Предположим, что безрисковая ставка составляет 5% для всех периодов. Предположим, каждые три месяца базовая цена может двигаться на 20% вверх или вниз, что дает нам u = 1,2, d = 0,8, t = 0,25 и трехступенчатое биномиальное дерево.
Изображение Сабрины Цзян © Investopedia 2020
Красный цвет указывает на базовые цены, а синий — на выплату пут-опционов.
Нейтральная к риску вероятность «q» равна 0,531446.
Используя указанное выше значение q и значения выплат при t = девять месяцев, соответствующие значения при t = шесть месяцев вычисляются как:
Изображение Сабрины Цзян © Investopedia 2020
Далее, используя эти вычисленные значения при t = 6, значения при t = 3, затем при t = 0 равны:
Изображение Сабрины Цзян © Investopedia 2020
Таким образом, текущая стоимость пут-опциона равна 2 долларам.18, что довольно близко к тому, что вы найдете при вычислениях с использованием модели Блэка-Шоулза (2,30 доллара США).
Итог
Хотя использование компьютерных программ может облегчить эти интенсивные вычисления, прогнозирование будущих цен остается основным ограничением биномиальных моделей для ценообразования опционов. Чем точнее временные интервалы, тем сложнее предсказать выплаты в конце каждого периода с высокой точностью.
Тем не менее, гибкость, позволяющая учитывать изменения, ожидаемые в разные периоды, является плюсом, что делает его подходящим для ценообразования американских опционов, включая оценки с ранним исполнением.
Значения, вычисленные с использованием биномиальной модели, близко совпадают со значениями, вычисленными на основе других широко используемых моделей, таких как модели Блэка-Шоулза, что указывает на полезность и точность биномиальных моделей для ценообразования опционов. Биномиальные модели ценообразования могут быть разработаны в соответствии с предпочтениями трейдера и могут работать как альтернатива модели Блэка-Шоулза.
Формула
, что это такое и как ее использовать в простых шагах
Состав:
- Что такое биномиальное распределение?
- Распределение Бернулли
- Формула биномиального распределения
- Рабочие примеры
Биномиальное распределение можно рассматривать как просто вероятность УСПЕХА или НЕУДАЧИ в эксперименте или опросе, который повторяется несколько раз.Биномиальное распределение — это тип распределения, который имеет два возможных результата (префикс «би» означает два или два). Например, подбрасывание монеты имеет только два возможных результата: орел или решка, а сдача теста может иметь два возможных результата: сдан или не пройден.
Биномиальное распределение показывает либо (S) успех, либо (F) недостаток.
- Первая переменная в биномиальной формуле, n, обозначает количество запусков эксперимента.
- Вторая переменная p представляет вероятность одного конкретного результата.
Например, предположим, что вы хотите узнать вероятность получения 1 при броске кубика. если вы бросили кубик 20 раз, вероятность того, что кубик выпадет при любом броске, равна 1/6. Бросьте двадцать раз, и вы получите биномиальное распределение (n = 20, p = 1/6). УСПЕХ будет означать «выбросить один», а НЕИСПРАВНОСТЬ — это «выбросить что-нибудь еще». Если бы рассматриваемый результат представлял собой вероятность выпадения кубика на четное число, тогда биномиальное распределение стало бы (n = 20, p = 1/2). Это потому, что ваша вероятность выпадения четного числа равна половине.
Критерии
Биномиальные распределения также должны соответствовать следующим трем критериям:
- Количество наблюдений или испытаний фиксировано. Другими словами, вы можете рассчитать вероятность того, что что-то произойдет, только если вы сделаете это определенное количество раз. Это здравый смысл — если вы подбрасываете монету один раз, вероятность выпадения решки составляет 50%. Если вы подбросите монету 20 раз, ваша вероятность получить решку очень, очень близка к 100%.
- Каждое наблюдение или испытание независимых.Другими словами, ни одно из ваших испытаний не влияет на вероятность следующего испытания.
- Вероятность успеха (решка, решка, неудача или пас) равна точно так же от одной попытки к другой.
Как только вы узнаете, что ваше распределение биномиально, вы можете применить формулу биномиального распределения для вычисления вероятности.
Нужна помощь с формулой? Chegg.com подберет для вас живого репетитора, и ваши первые 30 минут будут бесплатными!
Биномиальное распределение тесно связано с распределением Бернулли.Согласно Университету штата Вашингтон: «Если каждое испытание Бернулли является независимым, то количество успехов в следах Бернулли имеет биномиальное распределение. С другой стороны, распределение Бернулли — это биномиальное распределение с n = 1 ».
Распределение Бернулли — это набор испытаний Бернулли. Каждое испытание Бернулли имеет один возможный исход, выбираемый из S — успех или F — неудача. В каждом испытании вероятность успеха P (S) = p одинакова. Вероятность неудачи составляет всего 1 минус вероятность успеха: P (F) = 1 — p.(Помните, что «1» — это полная вероятность возникновения события… вероятность всегда находится между нулем и 1). Наконец, все испытания Бернулли независимы друг от друга, и вероятность успеха не меняется от испытания к испытанию, даже если у вас есть информация о результатах других испытаний.
Что такое биномиальное распределение? Примеры из реальной жизни
В реальной жизни можно найти множество примеров биномиальных распределений. Например, если новое лекарство вводится для лечения болезни, оно либо лечит болезнь (это успешно), либо не лечит болезнь (это неудача).Если вы покупаете лотерейный билет, вы либо выиграете, либо нет. По сути, все, что вы можете придумать, может быть только успехом или неудачей, может быть представлено биномиальным распределением.
Биномиальное распределение показывает либо (S) успех, либо (F) недостаток.
Формула биномиального распределения:
b (x; n, P) = n C x * P x * (1 — P) n — x
Где:
b = биномиальная вероятность
x = общее количество «успехов» (пас или неудача, орел или решка и т. Д.)
P = вероятность успеха в отдельном испытании
n = количество испытаний
Примечание: Формулу биномиального распределения также можно записать немного по-другому, потому что n C x = n! / х! (п — х)! (в этой формуле биномиального распределения используются факториалы (что такое факториал?). «q» в этой формуле — это просто вероятность неудачи (вычтите вероятность успеха из 1).
Формула биномиального распределения может вычислить вероятность успеха для биномиальных распределений.Часто вам говорят «вставить» числа в формулу и вычислить . Это легко сказать, но не так-то просто сделать — если вы не будете очень внимательны с порядком операций, вы не получите правильного ответа. Если у вас есть Ti-83 или Ti-89, калькулятор может сделать большую часть работы за вас. Если нет, вот как разбить проблему на простые шаги, чтобы каждый раз получать правильный ответ.
Пример 1
В. Монета подбрасывается 10 раз. Какова вероятность выпадения ровно 6 голов?
Я собираюсь использовать эту формулу: b (x; n, P) — n C x * P x * (1 — P) n — x
Количество испытаний (n) составляет 10
Шансы на успех («подбрасывание орлов») равны 0.4 = 210 * 0,015625 * 0,0625 = 0,205078125
Совет: Вы можете использовать калькулятор комбинаций , чтобы вычислить значение для n C x .
Как работать с формулой биномиального распределения: пример 2
80% людей, приобретающих страховку для домашних животных, — женщины. Если случайным образом выбраны 9 владельцев страховки для домашних животных, найдите с вероятностью, что именно 6 из них — женщины.
Шаг 1: Определите «n» из проблемы.В нашем примере вопроса n (количество случайно выбранных элементов) равно 9.
Шаг 2: Определите «X» из проблемы. X (число, которое вас просят найти вероятность) равно 6.
Шаг 3: Обработайте первую часть формулы. Первая часть формулы —
н! / (п — Х)! ИКС!
Подставьте свои переменные:
9! / ((9 — 6)! × 6!)
Что равняется 84. Отложите это число на мгновение.
Шаг 4: Найдите p и q.p — вероятность успеха, q — вероятность неудачи. Нам дают p = 80%, или 0,8. Таким образом, вероятность отказа составляет 1 — 0,8 = 0,2 (20%).
Шаг 5: Обработайте вторую часть формулы.
p X
= 0,8 6
= 0,262144
Отложите это число на мгновение.
Шаг 6: Обработайте третью часть формулы.
q (n — X)
= 0,2 (9-6)
= 0,2 3
=.008
Шаг 7: Умножьте ответ из шагов 3, 5 и 6 вместе.
84 × 0,262144 × 0,008 = 0,176.
Пример 3
60% покупателей спорткаров — мужчины. Если случайным образом выбрано 10 владельцев спортивных автомобилей, найдите с вероятностью, что именно 7 из них — мужчины.
Шаг 1: : Определите «n» и «X» из проблемы. Используя наш примерный вопрос, n (количество случайно выбранных элементов — в данном случае случайным образом выбираются владельцы спортивных автомобилей) равно 10, а X (число, которое вам предлагается «найти вероятность») равно 7.
Шаг 2: Вычислите первую часть формулы, а именно:
н! / (п — Х)! ИКС!
Подставляем переменные:
10! / ((10-7)! × 7!)
Что равняется 120. Отложите это число на мгновение.
Шаг 3: Найдите «p» — вероятность успеха и «q» — вероятность неудачи. Нам дан p = 60%, или 0,6. следовательно, вероятность отказа составляет 1 — 0,6 = 0,4 (40%).
Шаг 4: Выполните следующую часть формулы.
p X
= .6 7
= .0,0279936
Отложите это число, пока вы работаете с третьей частью формулы.
Шаг 5: Обработайте третью часть формулы.
q (0,4-7)
= 0,4 (10-7)
= 0,4 3
= 0,064
Шаг 6: Умножьте три ответа из шагов 2, 4 и 5 вместе.
120 × 0,0279936 × 0,064 = 0,215.
Вот и все!
Ссылки
Бейер, В.H. Стандартные математические таблицы CRC, 28-е изд. Бока-Ратон, Флорида: CRC Press, стр. 531, 1987.
Папулис, А. Вероятность, случайные величины и случайные процессы, 2-е изд. Нью-Йорк: Макгроу-Хилл, стр. 102-103, 1984.
Шпигель М. Р. Теория и проблемы вероятности и статистики. Нью-Йорк: McGraw-Hill, стр. 108-109, 1992.
Steinhaus, H. Mathematical Snapshots, 3-е изд. Нью-Йорк: Довер, 1999.
WSU. Получено 15 февраля 2016 г. с сайта: www.stat.washington.edu/peter/341/Hypergeometric%20and%20binomial.pdf
————————————————— —————————-
Нужна помощь с домашним заданием или контрольным вопросом? С помощью Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, оставьте комментарий на нашей странице в Facebook .
Биномиальные модели — Учебные заметки FRM
После прочтения вы сможете:
- Объясните концепцию безарбитражного и нейтрального по отношению к риску подхода к оценке производных ценных бумаг
- Поймите концепцию отсутствия арбитража при сравнении фактических и синтетических коллов или при сравнении фактических и синтетических пут.
- Понять концепции, лежащие в основе нейтрального с точки зрения риска подхода к оценке производных ценных бумаг в контексте модели ценообразования биномиальных опционов.
- Используйте модель ценообразования биномиальных опционов для расчета стоимости европейских и американских опционов колл и пут, а также стоимости азиатских и барьерных опционов.
- Варианты цены по однопериодной биномиальной модели на акцию без дивидендов.
- Распространите биномиальную модель на многопериодные параметры для определения цены как европейских, так и американских опционов колл и пут.
- Распространите биномиальную модель на другие базовые активы, включая фондовые индексы с непрерывными дивидендами, валюты и фьючерсные контракты.
Отсутствие арбитража и нейтральный к риску подход к оценке производных ценных бумаг
Арбитражное допущение
Арбитраж описывает ситуацию, когда инвестор может получить безрисковую торговую прибыль.
На данном рынке возможность арбитража существует, если
- Инвестор может в момент времени 0 заключить сделку, которая имеет нулевые первоначальные затраты, строго положительную вероятность будущей прибыли и нулевую вероятность будущих убытков
- Инвестор заключает сделку, которая дает ему / ей немедленную прибыль без риска будущих убытков
Другими словами, арбитраж — это практика использования дисбаланса цен на один и тот же актив, который существует между двумя или более рынками.Для деривативов это использование разницы в ценах на уникальный актив для получения безрисковой прибыли.
Если такая возможность существует, инвестор будет стремиться приумножить свои портфели, чтобы получить неограниченную прибыль. Однако в большинстве случаев это невозможно, так как другие активные участники рынка поступили бы так же. Таким образом, цены на рынке изменятся соответствующим образом, чтобы исключить возможность арбитража.
Например, рассмотрим акции компании ABC, которые торгуются на Нью-Йоркской фондовой бирже за 10 долларов.00, и эквивалент $ 11.00 на Лондонской фондовой бирже. Это создает прекрасную возможность безрискового арбитража. «Арбитражер» может купить акции ABC на Нью-Йоркской фондовой бирже за 10 долларов США и одновременно продать акции на Лондонской фондовой бирже за 11 долларов США, получив «безрисковую» прибыль в размере 1 доллара на акцию. Это действие участников рынка заставит две цены вернуться к одной цене.
Принцип отсутствия арбитража
Этот принцип просто утверждает, что на рынке просто не существует возможностей для арбитража.Это, в свою очередь, будет означать, что если любые два актива или комбинация активов (портфель) генерируют одинаковые платежи, они должны иметь одинаковую цену, в основном называемую законом единой цены .
Отсутствие арбитража с фактическими и синтетическими коллами
Фактический опцион колл дает право, но не обязанность купить данный базовый актив по указанной цене при наступлении срока погашения.
Синтетический колл, также известный как защитный пут, с другой стороны, представляет собой стратегию, при которой инвестор, владеющий базовыми активами / ценными бумагами, использует опцион пут в деньгах, чтобы имитировать эффективность опциона колл.{-rT} \) по безрисковой ставке, \ (r \) на покупку 1 единицы ценной бумаги по текущей рыночной цене \ (S_0 \)
Портфель B:
- Купить опцион колл со страйк-ценой \ (K \) со сроком погашения \ (T \).
Пусть \ (S_T \) будет базовой ценой ценной бумаги в момент времени \ (T \) В момент времени T выплата по портфелю A будет;
- 0 if \ (K> S_T \), и в этом случае инвестор исполняет пут, продав базовый актив, который стоит только \ (S_T \) при страйке \ (K \).Затем он использует это для погашения ссуды;
- \ (S_T-K \) if \ (K \ le S_T \), и в этом случае срок действия опциона истекает без денег, и инвестор продает актив по рыночной цене \ (S_T \), используя вырученные средства для погашения ссуду, а разницу оставляет себе.
Таким образом, комбинированная выплата составляет
$$ макс \ влево (0, S_T-K \ вправо) $$
Выплата из портфеля B будет либо 0, если \ (S_T
$$ макс (0, S_T-K) $$
Мы видим, что портфели A и B идентичны, и согласно закону одной цены, они оба должны иметь одинаковую цену.
Согласно предположению об отсутствии арбитража, стоимость создания портфеля A должна быть равна цене портфеля B, опциона колл. Портфель A известен как синтетический колл , потому что он имитирует выплату по опциону колл путем заимствования для покупки акций.
Синтетический колл позволяет инвестору извлечь выгоду из ожидаемого роста цены базового актива, ограничивая его / ее максимальный убыток премией, уплаченной при покупке пут.
Отсутствие арбитража с фактическими и синтетическими путями
Фактическая пут-опцион дает право, но не обязательство продать данный базовый актив по указанной цене при наступлении срока погашения.{-rT} \) в бескупонной ценной бумаге по беспроцентной ставке \ (r \).
Портфель B:
- Купить опцион пут с ценой исполнения K со сроком погашения T
Пусть \ (S_T \) будет ценой базовой ценной бумаги в момент времени \ (T \).
В момент \ (T \) выплата из портфеля A составит:
- 0 если \ (S_T> K \), и в этом случае инвестор исполнит колл, используя выручку от ценной бумаги для покупки базового актива по цене исполнения \ (K \), или;
- \ (K-S_T \) if \ (S_T
Таким образом, совокупный выигрыш от инвестора составит:
$$ макс \ влево (0, K-S_T \ вправо) $$
Выплата из портфеля B в момент \ (T \) будет либо равна 0, если \ (S_T> K \), либо \ (K-S_T \), если \ (S_T $$ макс \ влево (0, K-S_T \ вправо) $$ Мы видим, что портфели A и B идентичны, и согласно закону одной цены, они оба должны иметь одинаковую цену. Согласно предположению об отсутствии арбитража, стоимость создания портфеля A должна равняться цене портфеля B, опциона колл. Портфель A известен как синтетический пут , потому что он имитирует выплату по опциону пут, начиная с короткой позиции по акции и длинной позиции колл. Синтетический пут позволяет инвестору извлечь выгоду из ожидаемого снижения цены базового актива, ограничивая его / ее максимальный убыток премией, уплаченной при покупке опциона колл. Модель ценообразования биномиального варианта Нейтральный к риску подход к оценке производных ценных бумаг В предыдущем разделе мы рассмотрели сравнение фактических и синтетических коллов и путов и применение предположения об отсутствии арбитража. Репликация — это термин, используемый для описания позиции, созданной за счет наличия портфеля или комбинации ценных бумаг, которые имеют одинаковую выплату с опционом. В нашем случае синтетические опционы колл и пут (портфель А) можно назвать реплицирующими портфелями для описываемых фактических опционов колл и пут.{-rT} \) быть заимствованным или инвестированным в момент времени 0, и сколько единиц базовой ценной бумаги должно храниться для создания реплицирующего портфеля. Это приводит нас к упрощенному случаю, приведенному ниже. Предположим, что в момент времени \ (t = 0 \) цена акции равна \ (S_0 \). Мы предполагаем, что в течение одного периода цена акции может повышаться или понижаться. Следовательно, нам нужно найти значение производной в момент времени 0 на основе цены акции в момент времени 1, т.е.е. \ (S_1 \). Есть две возможности для цены акции в момент времени 1: $$ S_1 = \ begin {cases} S_0U, & \ text {если цена акции растет} \\ S_0D, & \ text {если цена акции снижается} \ end {ases} $$ Где U = величина коэффициента подъема больше 1. D = величина коэффициента движения вниз меньше 1. Возможности могут быть показаны с использованием биномиального дерева следующим образом: $$ \ begin {array} \ hline {} & {} & {S} _ {0} U \\ {S} _ {0} & {\ Huge \ begin {matrix} \ nearrow \\ \ searchrow \ end {matrix}} \\ {} & {} & {S} _ {0} D \\ \ end {array} $$ Рисунок 1: Однопериодное биномиальное дерево На рисунке выше представлена однопериодная биномиальная модель для цены акции. r \ end {align} $$ Это показывает, что, если мы принимаем нейтральные к риску вероятности восходящего или нисходящего движения цены акции, базовая акция растет с безрисковой нормой доходности, оправдывая нейтральный к риску подход к биномиальному ценообразованию опционов. Использование модели ценообразования биномиальных опционов для оценки стоимости опционов Пример 1: Однопериодная биномиальная модель Цена акции в момент времени 0 составляет 60 долларов. За один период цена акции может либо подняться до 90 долларов, либо упасть до 45 долларов. Безрисковая процентная ставка составляет 5% за период времени. Рассчитайте стоимость однопериодного европейского опциона колл \ (C_0 \) с ценой исполнения 75 $ . Решение Давайте сначала представим цену акций в биномиальном дереве: $$ \ begin {array} \ hline {} & {} & {{S} _ {1} = 90} \\ {{S} _ {0} = 60} & {\ Huge \ begin {matrix} \ nearrow \\ \ searchrow \ end {matrix}} & {} \\ {} & {} & {{S} _ {1} = 45} \\ \ end {array} $$ Мы также можем рассмотреть биномиальное дерево для соответствующих выплат, генерируемых опционом колл.{-0,05} [0,4017 × 15 + 0,5983 × 0] = 5,7316 \\ \ end {align *} $$ Чтобы сэкономить время и пространство, мы могли бы просто нарисовать одно биномиальное дерево с выплатой в конце периода, записанной под ценой акции, как показано ниже: $$ \ begin {array} \ hline {} & {} & \ begin {matrix} {{S} _ {1} = 90} \\ {C} _ {1} = \ text {max} (0 , 90–75) = 15} \ end {matrix} \\ \ begin {matrix} {{S} _ {0} = 60} \\ {{C} _ {0} =?} \ End {matrix} & {\ Huge \ begin {matrix} \ nearrow \\ \ searchrow \ end {matrix}} & {} \\ {} & {} & \ begin {matrix} {{S} _ {1} = 45} \\ { {C} _ {1} = \ text {max} (0,45-75) = 0} \ end {matrix} \\ \ end {array} $$ Следующая формула используется для определения цены опционов в биномиальной модели, в которой задана волатильность: \ (U \) = размер коэффициента перемещения вверх \ (= e ^ {(r- \ delta) t + \ sigma \ sqrt {t}} \) и \ (D \) = размер коэффициента движения вниз = \ (= e ^ {(r- \ delta) t- \ sigma \ sqrt {t}} \) \ (\ sigma \) — это годовая волатильность доходности базового актива, а t — длина шага в биномиальной модели. {(0.{0,05 × 1} -0,8869} {1,2461-0,8869} = 0,4576 \\ \ pi_D & = 1-0,4576 = 0,5424 \\ \ end {align *} $$ Таким образом, биномиальное дерево для цены акций выглядит следующим образом: $$ \ begin {array} \ hline {} & {} & \ begin {matrix} {{S} _ {1} = 30 \ times 1.2461 = $ 37,38} \\ {{C} _ {1} = \ text {max} (0,37.38-30) = $ 7.38} \ end {matrix} \\ \ begin {matrix} {{S} _ {0} = 30} \\ {{C} _ {0} =?} \ end {matrix} & {\ Huge \ begin {matrix} \ nearrow \\ \ searchrow \ end {matrix}} & {} \\ {} & {} & \ begin {matrix} {{S} _ {1} = 30 \ раз 0.{-0,05} [0,4576 × 7,38 + 0,5424 × 0] = 3,2124 доллара США Идеи, обсуждаемые в однопериодной биномиальной модели, применимы и здесь. Обратите внимание, что для простоты мы приняли периоды в годах. Однако это может быть и месяц. Этот раздел расширяет мыслительный процесс до двухпериодной модели, которая, как вы поймете, интуитивно понятна. Изучите следующую модель биномиального дерева, приведенную ниже, для цены акций. $$ \ begin {array} {} & {} & {} & {S} _ {2} = {S_1 U_1} \\ {} & {S} _ {1} = {S_0 U_0} & {\ Huge \ begin {matrix} \ nearrow \\ \ searchrow \ end {matrix}} & {} \\ {S} _ {0} \ begin {matrix} & {} & \\ & \ Huge \ nearrow & \\ & \ Огромный \ searchrow & \\ & {} & \ end {matrix} & {} & \ begin {matrix} {} \\ \\ {} \ end {matrix} & \ begin {matrix} {S} _ {2} = {S_1 D_1} \\ \\ {S} _ {2} = {S_1 U_1} \ end {matrix} \\ {} & {S} _ {1} = {S_0 D_0} & {\ Huge \ begin { матрица} \ nearrow \\ \ searchrow \ end {matrix}} & {} \\ {} & {} & {} & {S} _ {2} = {S_1 D_1} \\ \ end {array} $$ Рисунок 2: Двухэтапная биномиальная модель для цены акций (базового актива) Первый год двухпериодной биномиальной модели в основном совпадает с однопериодной биномиальной моделью.{-r} [\ pi_ {U_0} C_1 (U) + (1- \ pi_ {U_0}) C_1 (D)] $$ Значение в момент времени 1 — это просто ожидание в момент времени 1 выплаты по производному инструменту во время 2 на основе нейтральной с точки зрения риска меры вероятности. Используемые здесь обозначения могут немного сбивать с толку, но использование примера может помочь и, что наиболее важно, получить представление о транзакциях. Теперь изучите биномиальное дерево для выплаты ниже: $$ \ begin {array} {} & {} & {} & {C_2 (U_U)} \\ {} & {C} _ {1} (U) & \ begin {matrix} & {\ small {\ pi_ {U_1}}} & \\ & \ Huge \ nearrow & \\ & \ Huge \ searchrow & \\ & {\ small {1- \ pi_ {U_1}}} & \ end {matrix} & {} \\ {C} _ {0} \ begin {matrix} & {\ small {\ pi_ {U_0}}} & \\ & \ Huge \ nearrow & \\ & \ Huge \ searchrow & \\ & {\ small {1- \ pi_ {U_0}}} & \ end {matrix} & {} & \ begin {matrix} {} \\ \\ {} \ end {matrix} & \ begin {matrix} {{C_2 (U_D)}} \ \ \\ {{C_2 (D_U)}} \ end {matrix} \\ {} & {C} _ {1} (D) & \ begin {matrix} & {\ small {\ pi_ {U_2}}} & \\ & \ Huge \ nearrow & \\ & \ Huge \ searchrow & \\ & {\ small {1- \ pi_ {U_2}}} & \ end {matrix} & {} \\ {} & {} & { } & {{C_2 (D_D)}} \\ \ end {array} $$ Рисунок 3: Двухэтапная биномиальная модель для выплат по опционам Пример: оценка европейского опциона колл с использованием двухступенчатой биномиальной модели Цена акции в момент времени 0 составляет 60 долларов.За один период цена акции может либо подняться до 90 долларов, либо упасть до 45 долларов и. После восходящего движения в первом периоде цена акции может либо подняться до 120 долларов, либо упасть до 75 долларов. После нисходящего движения в первом периоде цена акции может либо подняться до 60 долларов, либо упасть до 37,50 долларов. Безрисковая процентная ставка составляет 5% за период времени. Рассчитайте стоимость двухпериодного европейского опциона колл \ (C_0 \) с ценой исполнения 75 долларов. Решение Рассмотрим следующее биномиальное дерево: $$ \ begin {array} {} & {} & {} & \ begin {matrix} S_ {UU} = 120 \\ C_ {UU} = 120-75 = 45 \ end {matrix} \\ {} & \ begin {matrix} {S} _ {U} = {90} \\ C_U =? \ end {matrix} & {\ Huge \ begin {matrix} \ nearrow \\ \ searchrow \ end {matrix}} & {} \\ \ begin {matrix} S_0 = 60 \\ C_0 =? \ end {matrix} \ begin {matrix} & {} & \\ & \ Huge \ nearrow & \\ & \ Huge \ searchrow & \\ & {} & \ end {matrix} & {} & \ begin {matrix} {} \\ \\ {} \ end {matrix} & \ begin {matrix} {\ begin {matrix} S_ {UD} = 75 \\ C_ {UD} = \ text {max} (0,75-75) = 0 \ end {matrix}} \\ \\ {\ begin {matrix} S_ {DU} = 60 \\ C_ {DU} = \ text {max} (0,60-75) = 0 \ end {matrix} } \ end {matrix} \\ {} & {\ begin {matrix} S_D = 45 \\ C_D =? \ end {matrix}} & {\ Huge \ begin {matrix} \ nearrow \\ \ searchrow \ end {matrix}} & {} \\ {} & {} & {} & {\ begin {matrix} S_ {DD } = 60 \\ C_ {DD} = \ text {max} (0,60-75) = 0 \ end {matrix}} \\ \ end {array} $$ Коэффициент движения для второго периода: $$ U_1 = \ cfrac {120} {90} = \ cfrac {4} {3} $$ и $$ D_1 = \ cfrac {75} {90} = \ cfrac {5} {6} $$ Теперь нейтральная к риску вероятность: $$ \ pi_1 = \ cfrac {e ^ {- r} -U_2} {U_2-D_2} = \ cfrac {e ^ {- 0.{-0,05} [0,40169 × 18,658 + (1-0,40169) × 0] \\ & = 7,1293 \\ \ end {align *} $$ Как вы, должно быть, поняли, когда выплаты равны нулю, это облегчает работу. Вы можете игнорировать их, чтобы сэкономить время. Кроме того, необходимо произвести соответствующую корректировку, если это была оферта. Пример: ценообразование европейского опциона пут с использованием двухступенчатой биномиальной модели Двухлетний европейский пут имеет цену исполнения 60 долларов по акциям при текущей цене 54 доллара. Была построена модель с двумя шагами, и ожидается, что цена акции будет повышаться или понижаться на 20% на каждом шаге.Размер каждого шага — один год. Постоянно рассчитываемая безрисковая ставка доходности, применяемая в течение срока действия контракта, составляет 4% годовых. Рассчитайте цену пут-опциона. Решение Рассмотрим следующее двухшаговое биномиальное дерево: $$ \ begin {array} {} & {} & {} & \ begin {matrix} S_ {UU} = 77.76 \\ P_ {UU} = max (60-77.76,0) = 0 \ end {matrix} \\ {} & \ begin {matrix} {S} _ {U} = {64.8} \\ P_U =? \ end {matrix} & {\ Huge \ begin {matrix} \ nearrow \\ \ searchrow \ end {matrix}} & {} \\ \ begin {matrix} S_0 = 54 \\ P_0 =? \ end {matrix} \ begin {matrix} & {} & \\ & \ Huge \ nearrow & \\ & \ Huge \ searchrow & \\ & {} & \ end {matrix} & {} & \ begin {matrix} {} \\ \\ {} \ end {matrix} & \ begin {matrix} {\ begin {matrix} P_ {UD} = 75 \\ P_ {UD} = \ text {max} (0,60-51.84) = 8.16 \ end {matrix}} \\ \\ {\ begin {matrix} S_ {DU} = 51.84 \\ P_ {DU} = \ text {max} (60-51.84,0) = 8.16 \ end { matrix}} \ end {matrix} \\ {} & {\ begin {matrix} S_D = 43.2 \\ P_D =? \ end {matrix}} & {\ Huge \ begin {matrix} \ nearrow \\ \ searchrow \ end {matrix}} & {} \\ {} & {} & {} & {\ begin {matrix} S_ {DD } = 37,5 \\ P_ {DD} = \ text {max} (60-34,56,0) = 25,44 \ end {matrix}} \\ \ end {array} $$ Мы применяем те же принципы, что и в случае опциона колл. Однако мы должны отметить, что пут приводит к выплате, когда цена базового актива падает ниже цены исполнения.2 \) — вероятности достижения верхнего, среднего и нижнего узлов. Этот принцип будет сохраняться по мере добавления новых узлов. Увеличение числа шагов в биномиальной модели Биномиальные модели с одним или двумя шагами нереально просты. Предполагая, что только один или два шага дадут очень грубое приближение к цене опциона. На практике срок действия опциона делится на 30 или более временных шагов. На каждом этапе происходит биномиальное движение цены акций. По мере увеличения количества временных шагов модель биномиального дерева делает те же предположения о поведении курса акций, что и модель Блэка – Шоулза – Мертона. Когда биномиальное дерево используется для определения цены европейского опциона, цена сходится к цене Блэка – Шоулза – Мертона по мере увеличения количества временных шагов. Очевидно, легко увидеть, что построение биномиального дерева зависит от расчета выплаты опциона и нейтральной с точки зрения риска вероятности.На основании предоставленной информации. Как указывалось ранее, американские опционы исполняются до истечения срока их действия, поэтому необходимо построить соответствующие биномиальные деревья. Биномиальная модель для вариантов в американском стиле Опционы в американском стиле могут быть исполнены до истечения срока их действия. Биномиальная модель позволяет нам исследовать выплату от опциона в конце каждого узла и определить, в каком узле опцион приведет к максимальной выплате и, следовательно, к раннему исполнению. Пример: пут-опцион в американском стиле Двухлетний пут в американском стиле имеет страйк-цену 60 долларов за акцию при текущей цене 54 доллара. Была построена модель с двумя шагами, и ожидается, что цена акции будет повышаться или понижаться на 20% на каждом шаге. {0.{-0.04} \ left (0.602 \ times3.1203 + 0.398 \ times14.459 \ right) = 7.3338 $$ Выплата по опциону в этом узле составляет 6 долларов, поэтому раннее исполнение не является оптимальным. Для опций в американском стиле мы проверяем значение опции в каждом узле. Если значение опциона больше при исполнении, мы присваиваем значение этому узлу. В противном случае параметр остается неиспользованным, и мы работаем в обратном направлении по биномиальному дереву, как обычно. Те же принципы будут применяться к соответствующим опционам колл в американском стиле Варианты заграждения Барьерный опцион — это опцион, существование которого зависит от достижения ценой базового актива заранее определенного барьерного уровня.Это может быть: Эти типы исполняются только в том случае, если цена базового актива ниже заранее определенного значения в течение срока действия опциона.Тогда выплаты рассчитываются следующим образом: $$ \ text {Вызов} — \ text {и} — \ text {out option} = \ begin {cases} \ text {max} (0, S_ {T} -X), & \ text {если max} (S_ {1}, S_ {2},… S_ {T}) \ ge B \\ F, & \ text {if max} (S_ {1}, S_ {2},… S_ {T }) г.Разборные варианты Опцион этого типа может быть исполнен только в том случае, если цена базового актива выше, чем значение барьера. Выплаты распределяются следующим образом: $$ \ text {Позвонить} — \ text {и} — \ text {out option} = \ begin {cases} \ text {max} (0, S_ {T} -X), & \ text {если max} (S_ {1}, S_ {2},… S_ {T})> B \\ F, & \ text {если max} (S_ {1}, S_ {2},… S_ {T} ) \ le B \ end {cases} $$ $$ \ text {Положите} — \ text {и} — \ text {out option} = \ begin {cases} \ text {max} (0, X-S_ {T}), & \ text {if max} (S_ {1}, S_ {2},… S_ {T})> B \\ F, & \ text {if max} (S_ {1}, S_ {2},… S_ {T}) \ le B \ end {case} $$ II. пробивает , подразумевая, что он не имеет ценности до тех пор, пока базовый актив не достигнет определенной указанной цены (уровня барьера). Далее его можно подразделить на: а. Варианты комплектации: Этот тип барьерного опциона исполняется только тогда, когда цена базового актива выше определенного уровня, скажем, $ B в течение срока действия опциона. Пусть начальная цена опциона равна X, тогда выплаты по этому опциону при наступлении срока погашения равны: . $$ \ text {Вызов} — \ text {и} — \ text {in option} = \ begin {cases} \ text {max} (0, S_ {T} -X), & \ text {если max} (S_ {1}, S_ {2},… S_ {T}) \ ge B \\ 0, & \ text {if max} (S_ {1}, S_ {2},… S_ {T }) г.Готовые варианты Это типы барьерных опционов, которые исполняются только при наступлении срока погашения, если цена базового актива падает ниже определенного заранее определенного уровня барьера (B). Таким образом, цены на момент погашения составляют: . $$ \ text {Позвонить} — \ text {и} — \ text {in option} = \ begin {cases} \ text {max} (0, S_ {T} -X), & \ text {если max} (S_ {1}, S_ {2},… S_ {T}) \ le B \\ 0, & \ text {if max} (S_ {1}, S_ {2},… S_ {T })> B \ end {case} $$ $$ \ text {Положите} — \ text {и} — \ text {in option} = \ begin {cases} \ text {max} (0, X-S_ {T}), & \ text {if max} (S_ {1}, S_ {2},… S_ {T}) \ le B \\ 0, & \ text {if max} (S_ {1} , S_ {2},… S_ {T})> B \ end {case} $$ Биномиальная цена барьера аналогична таковой для стандартного опциона, только расчет выплат по опциону при наступлении срока погашения зависит от уровня барьера. Пример: модели биномиального ценообразования для барьерных опций Текущая цена акции сотрудничества 100 $. За три месяца цена акций может вырасти до 110 долларов или упасть до 90 долларов. Для этой акции установлен опцион колл «вниз и внутрь» со страйк-ценой 80 долларов и барьерной стоимостью 100 долларов. Используя однопериодное биномиальное дерево, рассчитайте цену опциона при безрисковой процентной ставке 5%. Решение Начнем с построения чертежа биномиального дерева: $$ \ begin {array} \ hline {} & {} & \ begin {matrix} {S} _ {1} = 110 \\ C_1 = \ text {max} (0, S_T-X), \ text { если max} (S_1, S_2,…, S_T) = B = 0 \ end {matrix} \\ \ begin {matrix} {S} _ {0} = 100 \\ C_0 =? \ end {matrix} & {\ Huge \ begin {matrix} \ nearrow \\ \ searchrow \ end {matrix}} & {} \\ {} & {} & \ begin {matrix} {S} _ {1} = 90 \\ C_1 = \ text {max} (0, S_T-X), \ text {if max} (S_1, S_2,…, S_T) Напомним, что нижний и нижний порог срабатывает при наступлении срока погашения, если цена базового актива падает ниже определенного заранее определенного уровня барьера (B), а цена акции должна быть меньше, чем значение барьера, и больше, чем цена исполнения, в противном случае она будет бесполезный.{-0,05 × 0,5} [0,56 × 0 + 0,44 × 10] = 4,29 $$ Как вы, должно быть, поняли, вы можете легко расширить ценообразование на двухпериодную биномиальную модель. Итак, в основном, если вы можете рассчитать выплаты на конечных узлах и работать в обратном направлении по дереву, как обычно. Также обратите внимание на опционы пут. Азиатские варианты В азиатском опционе выплата зависит от средней цены базового актива в течение определенного периода времени, в отличие от стандартных опционов, где выплата определяется участием базового актива в определенный момент времени.{rt} -D} {U-D} $$ Репликация
Биномиальная модель одного периода
Двухпериодная биномиальная модель
Биномиальная модель для барьерных и азиатских опционов
Пример: ценообразование на азиатский вариант с использованием биномиальных моделей
Текущая цена акции — 100 долларов США. {\ frac {(0.{0,08 \ times0,5} -0,84187} {1,2868-0,84187} = 0,4471 $$
и
$$ 1- \ pi_u = 1-0,4471 = 0,5529 $$
Теперь мы можем удобно построить биномиальное дерево периодов:
$$ \ begin {array} \ hline {} & {} & {} & {} & {S} _ {2} = 165,59 \\ {} & {} & {S} _ {1} = 100 \ times 1,2868 = 128,68 & {\ Огромная \ begin {matrix} \ nearrow \\ \ searchrow \ end {matrix}} & {} \\ \ begin {matrix} {S} _ {0} = 100 \\ V_0 =? \ end {matrix} & {\ begin {matrix} \\ \ begin {matrix} \ begin {matrix} \ Huge \ nearrow \\ \ end {matrix} \\ \ Huge \ searchrow \ end {matrix} \\ \ end {matrix}} & {} & {} & {S} _ {2} = 108.34 \\ {} & {} & {S} _ {1} = 100 \ times 0.8419 = 84.19 & {\ Huge \ begin {matrix} \ nearrow \\ \ searchrow \ end {matrix}} & {} \\ { } & {} & {} & {} & {S} _ {2} = 70,84 \\ \ end {array} $$
Из дерева выше, две возможные цены в первый год: 128,68 и 84,19 и 165,59,108,34 и 10,87 в прошлом году. Возможные средние значения:
\ (\ cfrac {128,68 + 165,59} {2} = 147,135, \ cfrac {128,68 + 108,34} {2} = 118,51, \ cfrac {84,19 + 70,84} {2} = 77,515 \)
и \ (\ cfrac {84.2 \ times47.135 + 0.841872 \ times0.4471 \ times0.5529 \ times18.51 \ right) = 12.927.14681 $$
Мы можем легко перейти от среднего арифметического к геометрическому, который теперь должен быть интуитивно понятным. Более того, если нам не дана волатильность, мы могли бы легко скорректировать формулу, опуская ее.
Опции прочих активов
Подобно опционам на цены акций, мы можем построить биномиальные деревья для других активов, таких как фондовые индексы с непрерывными дивидендами, валюты и фьючерсные контракты.{q \ nabla t- \ sigma \ sqrt {\ Delta t}} $$
Пример: оценка опциона с использованием биномиальных моделей с учетом волатильности
Акция в настоящее время стоит 81 доллар и имеет дивидендную доходность 2%. На эти акции был выпущен годовой европейский опцион колл со страйк-ценой 80 долларов. Безрисковая ставка доходности, рассчитываемая непрерывно, составляет 4%, а волатильность акции — 20%.
Рассчитайте цену звонка, используя двухпериодное биномиальное дерево.
Решение
Построим биномиальное дерево следующим образом:
$$ \ begin {array} {} & {} & {} & \ begin {matrix} \ text {Узел D:} \\ S_ {UU} = 107.48 \\ C_ {UU} = max (107,48-80,0) = 27,48 \ end {matrix} \\ {} & \ begin {matrix} B \\ {S} _ {U} = 93,30 \\ C_U =? \ end {matrix} & {\ Huge \ begin {matrix} \ nearrow \\ \ searchrow \ end {matrix}} & {} \\ \ begin {matrix} A \\ S_0 = 81 \\ C_0 =? \ end {matrix} \ begin {matrix} & {} & \\ & \ Huge \ nearrow & \\ & \ Huge \ searchrow & \\ & {} & \ end {matrix} & {} & \ begin {matrix} {} \\ \\ {} \ end {matrix} & \ begin {matrix} {\ begin {matrix} \ text {Узел E:} \\ S_ {UD} = 81 \\ C_ {UD} = \ text { max} (81-80, 0) = 1 \ end {matrix}} \\ \\ {\ begin {matrix} \ text {Узел F:} \\ S_ {DU} = 81 \\ C_ {DU} = \ текст {max} (81-80) = 1 \ end {matrix}} \ end {matrix} \\ {} & {\ begin {matrix} C \\ S_D = 70.2 \ times27.48 + 2 \ times0.5002 \ times0.4998 \ times1 + 0 \ right] \\ & = \ $ 7.086 \ end {align} $$
Опционы на валюты
Иностранная валюта может рассматриваться как актив, обеспечивающий доход по безрисковой иностранной процентной ставке \ (r_f \).
Такие опционы характеризуются двумя безрисковыми нормами доходности, применимыми в юрисдикциях, которым принадлежит валюта.
Например, учитывая, что безрисковая ставка доходности в Австралии составляет 7%, безрисковая ставка в США составляет 5%, и один австралийский доллар обменивается на 0.2C (D_D) \ right] \ end {align} $$
Пример: биномиальная модель валютных опционов
Доллар США в настоящее время стоит 0,83 евро. Обменный курс между двумя валютами подвержен колебаниям в 15%. Безрисковая ставка доходности в США составляет 6%, а безрисковая ставка в Европе — 4%. На этой бирже был выписан 6-месячный европейский опцион колл со страйк-ценой 0,85 евро. {0.2 \ times0.114 + 2 \ times0.4482 \ times \ left (1-0.4482 \ right) \ times0 \ right] \\ & = \ $ 0,0229 \ end {align} $$
Опционы на фьючерсные контракты
У инвестора нет затрат на открытие логарифмической или короткой позиции по фьючерсному контракту. Отсюда следует, что в мире, нейтральном к риску, будущая цена должна иметь нулевой ожидаемый темп роста. Используя те же обозначения для недивидендных акций, как обсуждалось выше, и пусть \ (F_0 \) — начальная цена фьючерса, ожидаемая будущая цена в конце одного периода продолжительностью \ (\ Delta t \) также должна быть \ ( F_0 \), то следует, что:
$$ \ pi F_0 U + (1- \ pi) F_0 D = F_0 $$
Где
\ (\ pi = \ cfrac {1-D} {U-D} \)
Пример: опцион на фьючерсный контракт
Инвестор приобрел годовой опцион колл на базовый фьючерсный контракт.Текущая цена фьючерса — 40 долларов. За два 6-месячных шага цена фьючерса может вырасти или понизиться на 10%. Цена исполнения опциона колл составляет 42 доллара США, а безрисковая ставка доходности, рассчитываемая на протяжении всего срока действия контракта, составляет 5% годовых.
Рассчитайте цену опциона колл.
Решение
Рассмотрим следующее биномиальное дерево:
$$ \ begin {array} {} & {} & {} & \ begin {matrix} \ text {Узел D:} \\ F_ {UU} = 48.4 \\ C_ {UU} = max (48,4-42,0) = 6,40 \ end {matrix} \\ {} & \ begin {matrix} B \\ {F} _ {U} = 44 \\ C_U =? \ end {matrix} & {\ Huge \ begin {matrix} \ nearrow \\ \ searchrow \ end {matrix}} & {} \\ \ begin {matrix} A \\ F_0 = 40 \\ C_0 =? \ end {matrix} \ begin {matrix} & {} & \\ & \ Huge \ nearrow & \\ & \ Huge \ searchrow & \\ & {} & \ end {matrix} & {} & \ begin {matrix} {} \\ \\ {} \ end {matrix} & \ begin {matrix} {\ begin {matrix} \ text {Узел E:} \\ F_ {UD} = 39,6 \\ C_ {UD} = \ text { max} (39,6-42, 0) = 0 \ end {matrix}} \\ \\ {\ begin {matrix} \ text {Узел F:} \\ F_ {DU} = 39.6 \\ C_ {DU} = \ text {max} (39.6-42,0) = 0 \ end {matrix}} \ end {matrix} \\ {} & {\ begin {matrix} C \\ F_D = 36 \\ C_D =? \ end {matrix}} & {\ Huge \ begin {matrix} \ nearrow \\ \ searchrow \ end {matrix}} & {} \\ {} & {} & {} & {\ begin {matrix} \ text { Узел G:} \\ F_ {DD} = 32,4 \\ C_ {DD} = \ text {max} (32,4–42,0) = 0 \ end {matrix}} \\ \ end {array} $$
Учитывая процентное увеличение, значения U и D определяются как:
$$ \ begin {align} U & = 1.1 \\ D & = 0.9 \ end {align} $$
Затем мы вычисляем нейтральные к риску вероятности
$$ \ pi = \ frac {1-0.2 \ times6.4 \ right] \\ & = \ $ 1.52 \ end {align} $$
Обратите внимание, что мы вычислили цену на основе увеличения форвардной цены только за два шага, потому что все остальные узлы приводят к нулевой выплате.
Биномиальное распределение
4.3 Биномиальное распределение
Цели обучения
- Изучить понятие биномиальной случайной величины.
- Чтобы научиться распознавать случайную величину как биномиальную случайную величину.
Эксперимент по трехкратному подбрасыванию честной монеты и эксперимент по наблюдению за половой принадлежностью в соответствии с порядком рождения детей в случайно выбранной семье из трех детей совершенно разные, но случайные величины, которые подсчитывают количество орлов при подбрасывании монеты и количество мальчиков в семье (при условии, что оба пола равновероятны) — одна и та же случайная величина с распределением вероятностей
х0123П (х) 0,1250,3750,3750,125
Гистограмма, которая графически иллюстрирует это распределение вероятностей, представлена на рисунке 4.4 «Распределение вероятностей для трех монет и трех детей». Общим для этих двух экспериментов является то, что мы проводим три идентичных и независимых испытания одного и того же действия, каждое испытание имеет только два исхода (орел или решка, мальчик или девочка), а вероятность успеха равна 0,5. каждое испытание. Генерируемая случайная величина называется биномиальной случайной величиной — случайной величиной, которая подсчитывает успехи в фиксированном количестве независимых, идентичных испытаний эксперимента с успехом / неудачей. с параметрами n = 3 и p = 0,5. Это всего лишь один случай из общей ситуации.
Рисунок 4.4 Распределение вероятностей для трех монет и трех детей
Определение
Предположим, случайный эксперимент имеет следующие характеристики.
- Есть n идентичных и независимых испытаний общей процедуры.
- Для каждого испытания существует ровно два возможных исхода, один из которых называется «успехом», а другой «неудачей».
- Вероятность успеха в любом одном испытании равна тому же числу p .
Тогда дискретная случайная величина X , которая подсчитывает количество успехов в испытаниях n , является биномиальной случайной величиной с параметрами n и p .Мы также говорим, что X имеет биномиальное распределение с параметрами n и p .
Следующие четыре примера иллюстрируют определение. Обратите внимание, что в каждом случае «успех» — это результат, который учитывается, а не результат, который мы предпочитаем или считаем лучше в каком-то смысле.
- Произвольная выборка из 125 студентов была выбрана из крупного колледжа, в котором доля студентов женского пола составляет 57%.Предположим, что X обозначает количество студенток в выборке. В этой ситуации имеется n = 125 идентичных и независимых испытаний общей процедуры, выбирая студентов случайным образом; для каждого испытания есть ровно два возможных исхода: «успех» (что мы считаем, чтобы студентка была женщиной) и «неудача»; и, наконец, вероятность успеха в одном испытании равна p = 0,57. X — биномиальная случайная величина с параметрами n = 125 и p = 0.57.
- Тест с несколькими вариантами ответов состоит из 15 вопросов, в каждом из которых есть пять вариантов. Неподготовленный учащийся, проходящий тест, отвечает на каждый из вопросов случайным образом, выбирая произвольный ответ из пяти предложенных. Предположим, что X обозначает количество правильных ответов учащегося. X — биномиальная случайная величина с параметрами n = 15 и p = 1 ∕ 5 = 0,20.
- При опросе 1000 зарегистрированных избирателей каждого избирателя спрашивают, намерен ли он голосовать за кандидата в королеву Титанию на предстоящих выборах.Предположим, что X обозначает количество избирателей в опросе, которые намереваются проголосовать за Королеву Титанию. X — это биномиальная случайная величина с n = 1000 и p , равная истинной доле избирателей (опрошенных или нет), которые намереваются проголосовать за Королеву Титании.
- Экспериментальное лекарство было дано 30 пациентам с определенным заболеванием. Предположим, что X обозначает количество пациентов, у которых развиваются серьезные побочные эффекты. X является биномиальной случайной величиной с n = 30 и p , равной истинной вероятности того, что пациент с основным заболеванием испытает серьезные побочные эффекты, если ему будет дано это лекарство.
Формула вероятности для биномиальной случайной величины
Часто наиболее сложным аспектом работы с проблемой, связанной с биномиальной случайной величиной, является признание того, что рассматриваемая случайная величина имеет биномиальное распределение. Как только это известно, вероятности можно вычислить по следующей формуле.
Если X — биномиальная случайная величина с параметрами n и p , то
Р (х) = п! Х! (П-х)! Pxqn-х
, где q = 1 − p и где для любого счетного числа m , m! (читать « м факториал ») определяется
0! = 1, 1! = 1, 2! = 1 · 2, 3! = 1 · 2 · 3
и в целом
м! = 1 · 2 · · · (м − 1) · м
Пример 7
Семнадцать процентов жертв финансового мошенничества лично знают виновного в мошенничестве.
- Используйте формулу для построения распределения вероятностей для числа X людей в случайной выборке из пяти жертв финансового мошенничества, которые лично знали преступника.
- Следователь ежедневно рассматривает пять дел о финансовых махинациях. Найдите наиболее частое количество случаев каждый день, когда жертва знала преступника.
- Следователь ежедневно рассматривает пять дел о финансовых махинациях.Найдите среднее количество случаев в день, когда жертва знала преступника.
Решение:
Случайная величина X является биномиальной с параметрами n = 5 и p = 0,17; q = 1 − p = 0,83. Возможные значения X : 0, 1, 2, 3, 4 и 5.
Р (0) = 5! 0! 5! (0,17) 0 (0,83) 5 = 1 · 2 · 3 · 4 · 5 (1) · (1 · 2 · 3 · 4 · 5) 1 · (0,393
43) = 0,393
43≈0,3939
P (1) = 5! 1! 4! (0.17) 1 (0,83) 4 = 1 · 2 · 3 · 4 · 5 (1) · (1 · 2 · 3 · 4) (0,17) · (0,47458321) = 5 · (0,17) · (0,47458321) = 0,4033957285≈ 0,4034
П (2) = 5! 2! 3! (0,17) 2 (0,83) 3 = 1 · 2 · 3 · 4 · 5 (1 · 2) · (1 · 2 · 3) (0,0289) · (0,571787) = 10 · (0,0289) · (0,571787) = 0,165246443 ≈0,1652Остальные три вероятности вычисляются аналогично, чтобы получить распределение вероятностей
х012345P (х) 0.39390.40340.16520.03380.00350.0001
Сумма вероятностей не равна 1 из-за округления.
Это распределение вероятности представлено гистограммой на рисунке 4.5 «Распределение вероятностей биномиальной случайной переменной в», которая графически показывает, насколько маловероятны события X = 4 и X = 5. Соответствующая полоса на гистограмме над цифрой 4 едва видна, если вообще видна, а полоса над 5 слишком коротка, чтобы ее можно было увидеть.
- Значение X , которое наиболее вероятно, составляет X = 1, поэтому наиболее частое количество случаев, наблюдаемых каждый день, когда жертва знала, что преступник — это один.
Среднее количество случаев в день, когда жертва знала преступника, составляет в среднем X , что составляет
.
μ = Σx P (x) = 0 · 0,3939 + 1 · 0,4034 + 2 · 0,1652 + 3 · 0,0338 + 4 · 0,0035 + 5 · 0,0001 = 0,8497
Специальные формулы для среднего и стандартного отклонения биномиальной случайной величины
Поскольку биномиальная случайная величина является дискретной случайной величиной, формулы для ее среднего значения, дисперсии и стандартного отклонения, приведенные в предыдущем разделе, применяются к ней, как мы только что видели в примечании 4.29 «Пример 7» в случае среднего. Однако для биномиальной случайной величины есть гораздо более простые формулы.
Если X — биномиальная случайная величина с параметрами n и p , то
μ = np σ2 = npq σ = npq
где q = 1 − p
Пример 8
Найдите среднее значение и стандартное отклонение случайной величины X из примечания 4.29 «Пример 7».
Решение:
Случайная величина X является биномиальной с параметрами n = 5 и p = 0,17, а q = 1 − p = 0,83. Таким образом, его среднее значение и стандартное отклонение составляют
.
μ = np = 5 · 0,17 = 0,85 (точно)
и
σ = npq = 5 · 0,17 · 0,83 = 0,7055≈0,8399
Кумулятивное распределение вероятностей биномиальной случайной величины
Чтобы разрешить более широкий круг более реалистичных задач, глава 12 «Приложение» содержит таблицы вероятностей для биномиальных случайных величин для различных вариантов выбора параметров n и p .Эти таблицы не являются распределениями вероятностей, которые мы видели до сих пор, а представляют собой кумулятивных распределений вероятностей. Вместо вероятности P (x) таблица содержит вероятность
.
P (X≤x) = P (0) + P (1) + · · · + P (x)
Это проиллюстрировано на Рисунке 4.6 «Суммарные вероятности». Введенная в таблицу вероятность соответствует площади заштрихованной области. Причина предоставления кумулятивной таблицы заключается в том, что в практических задачах, связанных с биномиальной случайной величиной, обычно искомая вероятность имеет форму P (X≤x) или P (X≥x).Кумулятивную таблицу намного проще использовать для вычисления P (X≤x), поскольку все индивидуальные вероятности уже вычислены и сложены. Одной таблицы достаточно как для P (X≤x), так и для P (X≥x), и ее также можно использовать для быстрого получения вероятностей формы P (x) благодаря следующим формулам. Первое — это правило вероятности дополнений.
Рисунок 4.6 Совокупные вероятности
Если X — дискретная случайная величина, то
P (X≥x) = 1 − P (X≤x − 1) и P (x) = P (X≤x) −P (X≤x − 1)
Пример 9
Учащийся сдает экзамен «верно / неверно» из десяти вопросов.
- Определите вероятность того, что учащийся ответит правильно на шесть вопросов, просто угадав ответ на каждый вопрос.
- Найдите вероятность того, что учащийся получит проходной балл 60% или выше, просто угадав.
Решение:
Пусть X обозначает количество вопросов, которые учащийся правильно отгадывает. Тогда X — это биномиальная случайная величина с параметрами n = 10 и p = 0.50.
Искомая вероятность равна P (6). Формула дает
Р (6) = 10! (6!) (4!) (. 5) 6,54 = 0,205078125
Используя таблицу,
P (6) = P (X≤6) −P (X≤5) = 0,8281−0,6230 = 0,2051
Учащийся должен правильно угадать не менее 60% вопросов, что составляет 0,60 · 10 = 6 вопросов. Искомая вероятность равна , а не P (6) (легко допустить ошибку), а
.
P (X≥6) = P (6) + P (7) + P (8) + P (9) + P (10)Вместо того, чтобы вычислять каждое из этих пяти чисел по формуле и складывать их, мы можем использовать таблицу для получения
P (X≥6) = 1 − P (X≤5) = 1−0.6230 = 0,3770
, что требует гораздо меньше работы и достаточной точности для данной ситуации.
Пример 10
Мастер по ремонту бытовой техники ежедневно обслуживает пять стиральных машин. Одна треть обращений в сервисный центр требует установки определенной детали.
- У мастера по ремонту сегодня только одна такая деталь на грузовике. Определите вероятность того, что сегодня будет достаточно одной детали, то есть не более одной стиральной машины, которую он обслуживает, потребует установки именно этой детали.
- Найдите минимальное количество таких запчастей, которое он должен брать с собой каждый день, чтобы вероятность того, что у него будет достаточно для дневных обращений за помощью, была не менее 95%.
Решение:
Пусть X обозначает количество обращений в службу поддержки сегодня, для которых требуется запчасть. Тогда X — это биномиальная случайная величина с параметрами n = 5 и p = 1 ∕ 3 = 0,3-.
Обратите внимание, что рассматриваемая вероятность — это не P (1), а скорее P ( X ≤ 1).Используя сводную таблицу распределения в главе 12 «Приложение»,
P (X≤1) = 0,4609
- Ответом будет наименьшее число x , такое, что запись в таблице P (X≤x) будет не меньше 0,9500. Поскольку P (X≤2) = 0,7901 меньше 0,95, двух частей недостаточно. Поскольку P (X≤3) = 0,9547 равно 0,95, трех частей будет достаточно как минимум в 95% случаев. Таким образом, необходимо минимум три.
Основные выводы
- Дискретная случайная величина X , которая подсчитывает количество успехов в n идентичных независимых испытаниях процедуры, которая всегда приводит к одному из двух результатов, «успеху» или «неудаче», и в которой вероятность успеха на каждом испытании один и тот же номер p , называется биномиальной случайной величиной с параметрами n и p .
- Существует формула для вероятности того, что биномиальная случайная величина с параметрами n и p примет конкретное значение x .
- Существуют специальные формулы для среднего, дисперсии и стандартного отклонения биномиальной случайной величины с параметрами n и p , которые намного проще, чем общие формулы, применимые ко всем дискретным случайным величинам.
- Таблицы кумулятивного распределения вероятностей, если они доступны, облегчают вычисление вероятностей, встречающихся в типичных практических ситуациях.
Упражнения
Определите, является ли случайная величина X биномиальной случайной величиной. Если да, укажите значения n и p . Если нет, объясните, почему нет.
- X — это количество точек на верхней грани брошенной матрицы.
- X — это количество червей в пятикарточной руке, вытянутой (без замены) из хорошо перетасованной обычной колоды.
- X — это количество дефектных деталей в выборке из десяти случайно выбранных деталей, поступающих в процессе производства, в котором 0,02% всех деталей являются дефектными.
- X — это количество точек на верхней грани справедливого кубика, которое равно шести броскам кубика.
- X — это количество кубиков, на верхней грани которых отображается четное количество точек при одновременном броске шести кубиков.
Определите, является ли случайная величина X биномиальной случайной величиной. Если да, укажите значения n и p . Если нет, объясните, почему нет.
- X — количество черных шариков в выборке из 5 шариков, взятых случайным образом и без замены из коробки, содержащей 25 белых шариков и 15 черных шариков.
- X — количество черных шариков в выборке из 5 шариков, вытянутых случайным образом и с заменой из коробки, содержащей 25 белых шариков и 15 черных шариков.
- X — это количество избирателей, проголосовавших за предложенный закон, в выборке из 1200 случайно выбранных избирателей, выбранных из всего электората страны, в которой за закон высказываются 35% избирателей.
- X — это количество рыб определенного вида среди следующих десяти, выловленных коммерческим рыболовным судном, которые имеют длину более 13 дюймов, когда 17% всей такой рыбы превышает 13 дюймов в длину.
- X — это количество монет, которые соответствуют хотя бы одной другой монете при одновременном подбрасывании четырех монет.
X — биномиальная случайная величина с параметрами n = 12 и p = 0,82. Вычислите указанную вероятность.
- п (11)
- П (9)
- П (0)
- П (13)
X — биномиальная случайная величина с параметрами n = 16 и p = 0.74. Вычислите указанную вероятность.
- п (14)
- П (4)
- П (0)
- П (20)
X — биномиальная случайная величина с параметрами n = 5, p = 0,5. Используйте таблицы в главе 12 «Приложение», чтобы вычислить указанную вероятность.
- P ( X ≤ 3)
- P ( X ≥ 3)
- П (3)
- П (0)
- П (5)
X — биномиальная случайная величина с параметрами n = 5, p = 0.3-. Используйте таблицу в главе 12 «Приложение», чтобы вычислить указанную вероятность.
- P ( X ≤ 2)
- P ( X ≥ 2)
- П (2)
- П (0)
- П (5)
X — биномиальная случайная величина с показанными параметрами.Используйте таблицы в главе 12 «Приложение», чтобы вычислить указанную вероятность.
- n = 10, p = 0,25, P ( X ≤ 6)
- n = 10, p = 0,75, P ( X ≤ 6)
- n = 15, p = 0,75, P ( X ≤ 6)
- n = 15, p = 0.75, П (12)
- n = 15, p = 0,6-, P (10≤X≤12)
X — биномиальная случайная величина с показанными параметрами. Используйте таблицы в главе 12 «Приложение», чтобы вычислить указанную вероятность.
- n = 5, p = 0,05, P ( X ≤ 1)
- n = 5, p = 0.5, пол. ( X ≤ 1)
- n = 10, p = 0,75, P ( X ≤ 5)
- n = 10, p = 0,75, P (12)
- n = 10, p = 0,6-, P (5≤X≤8)
X — биномиальная случайная величина с показанными параметрами.Воспользуйтесь специальными формулами для вычисления среднего значения μ и стандартного отклонения σ .
- n = 8, p = 0,43
- n = 47, p = 0,82
- n = 1200, p = 0,44
- n = 2100, p = 0,62
X — биномиальная случайная величина с показанными параметрами.Воспользуйтесь специальными формулами для вычисления среднего значения μ и стандартного отклонения σ .
- n = 14, p = 0,55
- n = 83, p = 0,05
- n = 957, p = 0,35
- n = 1750, p = 0,79
X — биномиальная случайная величина с показанными параметрами.Вычислите его среднее значение μ и стандартное отклонение σ двумя способами, сначала используя таблицы в главе 12 «Приложение» в сочетании с общими формулами μ = Σx P (x) и σ = [Σx2 P (x)] — μ2, затем по специальным формулам μ = np и σ = npq.
- n = 5, p = 0,3-
- n = 10, p = 0,75
X — биномиальная случайная величина с показанными параметрами.Вычислите его среднее значение μ и стандартное отклонение σ двумя способами, сначала используя таблицы в главе 12 «Приложение» в сочетании с общими формулами μ = Σx P (x) и σ = [Σx2 P (x)] — μ2, затем по специальным формулам μ = np и σ = npq.
- n = 10, p = 0,25
- n = 15, p = 0,1
X — биномиальная случайная величина с параметрами n = 10 и p = 1 ∕ 3.Используйте кумулятивное распределение вероятностей для X , приведенное в главе 12 «Приложение», чтобы построить распределение вероятностей X .
X — биномиальная случайная величина с параметрами n = 15 и p = 1 ∕ 2. Используйте кумулятивное распределение вероятностей для X , приведенное в главе 12 «Приложение», чтобы построить распределение вероятностей X .
В определенной настольной игре ход игрока начинается с трех бросков пары кубиков. Если игрок все три раза бросает удвоение, применяется штраф. Вероятность выпадения двойников при одном броске пары честных игральных костей составляет 1/6. Найдите вероятность выпадения удвоений все три раза.
Монета изогнута так, что вероятность того, что она упадет орлом, равна 2/3.Монета подбрасывается десять раз.
- Найдите вероятность того, что он выпадет один на один не более пяти раз.
- Найдите вероятность того, что он выпадет орлом больше раз, чем решка.
Базовый
Англоговорящий турист посещает страну, в которой 30% населения говорит по-английски.Ему нужно спросить у кого-нибудь дорогу.
- Определите вероятность того, что первый встречный человек сможет говорить по-английски.
- Турист видит четырех местных жителей, стоящих на автобусной остановке. Найдите вероятность того, что хотя бы один из них будет говорить по-английски.
Вероятность того, что яйцо в розничной упаковке треснет или сломано, равна 0.025.
- Найдите вероятность того, что в коробке с дюжиной яиц нет яиц, которые треснуты или разбиты.
- Найдите вероятность того, что картонная упаковка
в одной дюжине яиц есть (i) по крайней мере одно треснувшее или разбитое; (ii) по крайней мере
два, которые треснуты или сломаны. - Найдите среднее количество треснувших или разбитых яиц в одной дюжине картонных коробок.
Каждую неделю в магазине бытовой техники продается 20 холодильников.Десять процентов всех покупателей холодильника покупают расширенную гарантию. Пусть X обозначит количество следующих 20 покупателей, которые сделают это.
- Убедитесь, что X удовлетворяет условиям для биномиальной случайной величины, и найдите n и p .
- Найдите вероятность того, что X равно нулю.
- Найдите вероятность того, что X равно двум, трем или четырем.
- Найдите вероятность того, что X будет не меньше пяти.
Из-за неблагоприятных условий выращивания 5% грейпфрутов, выращиваемых в определенном регионе, были низкого качества. Грейпфруты продаются десятками.
- Найдите среднее количество грейпфрутов низкого качества на дюжину коробок.
- Коробка, содержащая два или более грейпфрута низкого качества, вызовет сильную негативную реакцию покупателей. Найдите вероятность того, что коробка с дюжиной грейпфрутов будет содержать два или более грейпфрута низкого качества.
Вероятность того, что моток 7 унций камвольной пряжи со скидкой содержит узел, равна 0.25. Гонерил покупает десять мотков, чтобы связать плед.
- Найдите вероятность того, что (i) ни один из
десять мотков будут содержать узел; (ii) самое большее одно завещание. - Найдите ожидаемое количество мотков, содержащих узлы.
- Найдите наиболее вероятное количество мотков с узлами.
- Найдите вероятность того, что (i) ни один из
Треть всех пациентов, которые проходят неинвазивный, но неприятный медицинский тест, нуждаются в седативном препарате.В лаборатории ежедневно проводится 20 таких тестов. Пусть X обозначает количество пациентов в любой день, которым требуется седативное средство.
- Убедитесь, что X удовлетворяет условиям для биномиальной случайной величины, и найдите n и p .
- Найдите вероятность того, что в любой день от пяти до девяти пациентов потребуется седативное средство (включая пять и девять).
- Найдите среднее количество пациентов, которым ежедневно требуется седативное средство.
- Используя кумулятивное распределение вероятностей для X в главе 12 «Приложение», найдите минимальное количество x мин доз седативного средства, которое должно быть под рукой в начале дня, чтобы с вероятностью 99% лаборатория не кончится.
Около 2% выпускников жертвуют деньги после получения предложения от колледжа или университета, который они окончили.Найдите среднее количество денежных подарков, которые колледж может ожидать на каждые 2000 отправленных им запросов.
Из всех студентов колледжей, имеющих право сдавать кровь, около 18% делают это на регулярной основе. Каждый месяц местный банк крови присылает призыв сдать кровь 250 случайно выбранным студентам. Найдите среднее количество апелляций в таких рассылках, адресованных студентам, которые уже сдают кровь.
Около 12% всех людей пишут левой рукой. Класс из 130 студентов встречается в классе со 130 отдельными партами, 14 из которых предназначены для людей, которые пишут левой рукой. Найдите вероятность того, что ровно 14 учащихся в классе будут писать левой рукой.
65% своих звонков коммивояжер продает постоянным клиентам.Он делает четыре звонка в день по продажам.
- Постройте распределение вероятностей X , количество продаж, совершаемых за день.
- Найдите вероятность того, что в случайно выбранный день продавец совершит продажу.
- Предполагая, что продавец совершает 20 торговых звонков в неделю, найдите среднее значение и стандартное отклонение количества продаж, совершенных в неделю .
Корпорация провела масштабную рекламу, пытаясь гарантировать, что более половины взрослого населения узнает торговую марку ее продуктов.В случайной выборке из 20 взрослых 14 узнали его торговую марку. Какова вероятность того, что 14 или более человек в такой выборке узнали бы его торговую марку, если бы фактическая доля p всех взрослых, узнающих торговую марку, составляла всего 0,50?
Приложения
При падении на твердую поверхность канцелярская кнопка падает острым концом на поверхность с вероятностью 2/3; он приземляется острием, направленным вверх с вероятностью 1/3.Галс сбрасывается, и его положение приземления проверяется 15 раз.
- Найдите вероятность того, что он приземлится острием в воздухе не менее 7 раз.
- Если эксперимент по 15 раз сбрасывать галс повторяется неоднократно, каково среднее количество раз, когда он приземляется острием в воздухе?
Профессиональный корректор с вероятностью 98% обнаружит ошибку в письменной работе (кроме орфографических ошибок, двойных слов и подобных ошибок, обнаруживаемых машиной).Работа содержит четыре ошибки.
- Найдите вероятность того, что корректор пропустит хотя бы одно из них.
- Покажите, что два таких корректора, работающих независимо, с вероятностью 99,96% обнаружат ошибку в письменной работе.
- Найдите вероятность того, что два таких корректора, работающих независимо, пропустят хотя бы одну ошибку в работе, содержащей четыре ошибки.
Экзамен с несколькими вариантами ответов состоит из 20 вопросов; для каждого вопроса есть четыре варианта ответа.
- Студент угадывает ответ на каждый вопрос. Найдите шанс, что он угадает правильно от четырех до семи раз.
- Найдите минимальный балл, который может установить преподаватель, чтобы вероятность того, что учащийся сдаст результат, просто угадав, составляла 20% или меньше.
Несмотря на требование, чтобы все собаки, содержащиеся в питомнике, были вакцинированы, вероятность того, что у здоровой собаки, содержащейся в чистом, хорошо вентилируемом помещении, разовьется коновой кашель от носителя, составляет 0.008.
- Если перевозчика (конечно, не известного) посадили на борт с тремя другими собаками, какова вероятность того, что хотя бы у одной из трех здоровых собак разовьется коновой кашель?
- Если на переноске находятся четыре других собаки, какова вероятность того, что хотя бы у одной из четырех здоровых собак разовьется коновой кашель?
- Схема, очевидная из частей (а) и (b), заключается в том, что если вместе посадить K + 1 собак, одну перевозчика и K здоровых собак, то вероятность того, что хотя бы у одной из здоровых собак разовьется коновой кашель, составляет P (X≥1) = 1− (0.992) K, где X — биномиальная случайная величина, которая подсчитывает количество здоровых собак, у которых развивается это состояние. Поэкспериментируйте с различными значениями K в этой формуле, чтобы найти максимальное количество K + 1 собак, которых владелец питомника может вместе сесть, так что если у одной из собак есть заболевание, вероятность заражения другой собаки будет меньше 0,05.
Следователям необходимо определить, у кого из 600 взрослых есть заболевание, которым страдают 2% взрослого населения.У каждого человека берут образец крови.
- Покажите, что ожидаемое количество заболевших в группе из 600 человек составляет 12 человек.
- Вместо тестирования всех 600 образцов крови, чтобы найти 12 ожидаемых больных, исследователи группируют образцы в 60 групп по 10 человек в каждой, смешивают немного крови из каждого из 10 образцов в каждой группе и тестируют каждую из 60 смесей. . Докажите, что вероятность того, что любая такая смесь будет содержать кровь хотя бы одного больного человека, следовательно, положительный результат теста, составляет около 0.18.
- На основании результата (b) покажите, что ожидаемое количество смесей, дающих положительный результат, составляет около 11. (Предположим, что действительно 11 из 60 смесей дали положительный результат, тогда мы знаем, что ни один из 490 человек, чья кровь была в крови, была положительной. оставшиеся 49 образцов, которые дали отрицательный результат, были инфицированы. Мы исключили 490 человек из нашего поиска, выполнив только 60 тестов.)
Дополнительные упражнения
Ответы
- небиномиальный; не успех / неудача.
- небиномиальный; судебные процессы не являются независимыми.
- бином; n = 10, p = 0,0002
- бином; n = 6, p = 0,5
- бином; n = 6, p = 0,5
- 0.2434
- 0,2151
- 0,1812≈0
- 0
- 0,8125
- 0,5000
- 0,3125
- 0.0313
- 0,0312
- 0,9965
- 0,2241
- 0,0042
- 0,2252
- 0,5390
- мк = 3.44, σ = 1.4003
- мкм = 38,54, σ = 2,6339
- мкм = 528, σ = 17,1953
- мкм = 1302, σ = 22,2432
- мк = 1.6667, σ = 1,0541
- мкм = 7,5, σ = 1,3693
х0123P (х) 0,01730.08670.19510.2602
х4567P (х) 0.22760.13650.05690.0163
x8910P (x) 0,00300,00040.0000
- n = 20, p = 0.1
- 0,1216
- 0,5651
- 0,0432
Варианты
— Поиск вероятностей с использованием биномиальной модели
Давайте просто рассмотрим аспект вероятностей.{0,12 \ times 0,25} — 0,9} {1,1 — 0,9} = 0,6523 $
Теперь рассмотрим двухступенчатую модель. Акция окажется в одном из трех состояний.
- uu
- ud или du
- dd
Обратите внимание, что, поскольку умножение коммутативно, $ S \ times d \ times u = S \ times u \ times d $, и мы должны указать от 2 до 1 вниз и 1 вверх, не обращая внимания на то, что было первым: вниз или вверх. . (Это дерево , рекомбинирующее . Если у нас есть дивиденды, дерево не рекомбинирует и становится более сложным.3 $ 903 18
Коэффициенты 1, 3, 3, 1 соответствуют различным путям перехода к конечным состояниям, а именно
- {uuu}
- {uud, udu, duu}
- {udd, dud, ddu}
- {ddd}
Множители — это функция выберите , которую вы описали в своем вопросе. Другой способ подумать об этом — через треугольник Паскаля.
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
Как только вы разберетесь с шаблоном, его будет довольно легко расширить.
Есть гораздо лучший график, чем я могу нарисовать, и никакое обсуждение биномиальных деревьев вариантов не было бы полным без него. В то время как есть 3 пути к каждому из средних ящиков в крайнем правом углу, есть только 1 путь к верхнему ящику.
Понимание Бернулли и биномиальных распределений | Валентина Альто
Всякий раз, когда вы имеете дело со случайными переменными, важно определить связанную с ними функцию вероятности. Последняя — это функция, которая присваивает каждому возможному результату вашей случайной переменной X число от 0 до 1.Это число представляет собой вероятность, связанную с этим результатом, и описывает вероятность появления результата.
Среди дискретных случайных величин (что означает, что поддержка случайной величины — это счетное число значений), вероятно, наиболее важными распределениями вероятностей являются распределения Бернулли и биномиальные распределения.
В этой статье я собираюсь объяснить идею каждого распределения, их соответствующие значения (ожидаемые значения и дисперсия) с доказательствами и примерами.
Распределение Бернулли
Распределение Бернулли — это дискретное распределение вероятностей случайной величины, которое принимает двоичный логический вывод: 1 с вероятностью p и 0 с вероятностью (1-p). Идея состоит в том, что всякий раз, когда вы проводите эксперимент, который может привести либо к успеху, либо к провалу, вы можете связать с вашим успехом (обозначенным цифрой 1) вероятность p, в то время как ваша неудача (помечена 0) будет иметь вероятность ( 1-п).
Функция вероятности, связанная с переменной Бернулли, имеет следующий вид:
Вероятность успеха p является параметром распределения Бернулли, и если дискретная случайная величина X следует за этим распределением, мы пишем:
Представьте, что ваш эксперимент состоит из подбрасывая монету, и вы выиграете, если на выходе окажется решка.Кроме того, поскольку монета справедливая, вы знаете, что вероятность выпадения хвоста равна p = 1/2. Следовательно, установив tail = 1 и head = 0, вы можете вычислить вероятность успеха следующим образом:
Опять же, представьте, что вы собираетесь бросить кости, и вы ставите свои деньги на число 1: следовательно, число 1 будет будет вашим успехом (помечено 1), а любое другое число будет неудачей (помечено 0). Вероятность успеха 1/6. Если вы хотите вычислить вероятность отказа, сделайте так:
Наконец, давайте вычислим ожидаемое значение (EV) и дисперсию.Зная, что EV и V дискретной случайной величины задаются формулами:
Отсюда следует, что для случайной величины Бернулли X :
Итак, идея распределения Бернулли состоит в том, что эксперимент повторяется только один раз. Но что произойдет, если мы проведем более одного испытания в предположении, что испытания независимы друг от друга?
Биномиальное распределение
Ответ на этот вопрос — биномиальное распределение. Это распределение описывает поведение результатов n случайных экспериментов, каждый из которых имеет распределение Бернулли с вероятностью p .
Давайте вспомним предыдущий пример подбрасывания справедливой монеты. Мы сказали, что наш эксперимент состоял в том, чтобы один раз подбросить эту монету. Давайте немного изменим его и скажем, что мы собираемся подбросить эту монету 5 раз. Среди этих испытаний у нас будут несколько успешных (хвост, обозначенный как 1) и несколько неудачных (голова, обозначенный как 0). Каждое испытание имеет вероятность 1/2 успеха и 1/2 неудачи. Нам может быть интересно узнать, какова вероятность получения заданного числа x успехов.Как мы будем действовать?
Давайте визуализируем этот эксперимент:
Итак, мы подбросили нашу монету 5 раз и проиграли в первых 3 попытках, а выиграли в последних 2. Поскольку мы сказали, что успех = хвост = 1 и неудача = голова = 0, мы можно перефразировать следующим образом:
Теперь каждое испытание является случайной величиной Бернулли, следовательно, вероятность его появления равна p, если она равна 1, в противном случае — 0. Следовательно, если мы хотим вычислить вероятность ex ante того, что имея вышеуказанную ситуацию (3 неудачи и 2 успеха), у нас будет что-то вроде этого:
И поскольку испытания независимы друг от друга:
Обобщая это рассуждение, если бы у нас было n испытаний с x успехами:
Теперь необходимо представить следующую концепцию.Действительно, до сих пор мы вычисляли вероятность двух успехов точно в указанном выше порядке. Тем не менее, поскольку мы заинтересованы в том, чтобы иметь заданное количество успехов независимо от того, в каком порядке они нам даны, мы должны принять во внимание все возможные комбинации достижения x успехов.
А именно, представьте, что мы подбрасываем монету 3 раза и хотим вычислить вероятность того, что из 3 попыток выпадет 1 решка. Следовательно, мы выиграем в одном из следующих сценариев:
Как видите, есть три различных комбинации результатов, которые приводят к успеху.



Добавить комментарий